Example 6: Solving Partial Differential Equation (PDE)
We aim to solve a 2D poisson equation \(\nabla^2 f(x,y) = -2\pi^2{\rm sin}(\pi x){\rm sin}(\pi y)\), with boundary condition \(f(-1,y)=f(1,y)=f(x,-1)=f(x,1)=0\). The ground truth solution is \(f(x,y)={\rm sin}(\pi x){\rm sin}(\pi y)\).
from kan import *
import matplotlib.pyplot as plt
from torch import autograd
from tqdm import tqdm
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)
dim = 2
np_i = 21 # number of interior points (along each dimension)
np_b = 21 # number of boundary points (along each dimension)
ranges = [-1, 1]
model = KAN(width=[2,2,1], grid=5, k=3, seed=1, device=device)
def batch_jacobian(func, x, create_graph=False):
# x in shape (Batch, Length)
def _func_sum(x):
return func(x).sum(dim=0)
return autograd.functional.jacobian(_func_sum, x, create_graph=create_graph).permute(1,0,2)
# define solution
sol_fun = lambda x: torch.sin(torch.pi*x[:,[0]])*torch.sin(torch.pi*x[:,[1]])
source_fun = lambda x: -2*torch.pi**2 * torch.sin(torch.pi*x[:,[0]])*torch.sin(torch.pi*x[:,[1]])
# interior
sampling_mode = 'random' # 'radnom' or 'mesh'
x_mesh = torch.linspace(ranges[0],ranges[1],steps=np_i)
y_mesh = torch.linspace(ranges[0],ranges[1],steps=np_i)
X, Y = torch.meshgrid(x_mesh, y_mesh, indexing="ij")
if sampling_mode == 'mesh':
#mesh
x_i = torch.stack([X.reshape(-1,), Y.reshape(-1,)]).permute(1,0)
else:
#random
x_i = torch.rand((np_i**2,2))*2-1
x_i = x_i.to(device)
# boundary, 4 sides
helper = lambda X, Y: torch.stack([X.reshape(-1,), Y.reshape(-1,)]).permute(1,0)
xb1 = helper(X[0], Y[0])
xb2 = helper(X[-1], Y[0])
xb3 = helper(X[:,0], Y[:,0])
xb4 = helper(X[:,0], Y[:,-1])
x_b = torch.cat([xb1, xb2, xb3, xb4], dim=0)
x_b = x_b.to(device)
steps = 20
alpha = 0.01
log = 1
def train():
optimizer = LBFGS(model.parameters(), lr=1, history_size=10, line_search_fn="strong_wolfe", tolerance_grad=1e-32, tolerance_change=1e-32, tolerance_ys=1e-32)
pbar = tqdm(range(steps), desc='description', ncols=100)
for _ in pbar:
def closure():
global pde_loss, bc_loss
optimizer.zero_grad()
# interior loss
sol = sol_fun(x_i)
sol_D1_fun = lambda x: batch_jacobian(model, x, create_graph=True)[:,0,:]
sol_D1 = sol_D1_fun(x_i)
sol_D2 = batch_jacobian(sol_D1_fun, x_i, create_graph=True)[:,:,:]
lap = torch.sum(torch.diagonal(sol_D2, dim1=1, dim2=2), dim=1, keepdim=True)
source = source_fun(x_i)
pde_loss = torch.mean((lap - source)**2)
# boundary loss
bc_true = sol_fun(x_b)
bc_pred = model(x_b)
bc_loss = torch.mean((bc_pred-bc_true)**2)
loss = alpha * pde_loss + bc_loss
loss.backward()
return loss
if _ % 5 == 0 and _ < 50:
model.update_grid_from_samples(x_i)
optimizer.step(closure)
sol = sol_fun(x_i)
loss = alpha * pde_loss + bc_loss
l2 = torch.mean((model(x_i) - sol)**2)
if _ % log == 0:
pbar.set_description("pde loss: %.2e | bc loss: %.2e | l2: %.2e " % (pde_loss.cpu().detach().numpy(), bc_loss.cpu().detach().numpy(), l2.cpu().detach().numpy()))
train()
cuda
checkpoint directory created: ./model
saving model version 0.0
pde loss: 2.23e+00 | bc loss: 5.99e-03 | l2: 3.78e-03 : 100%|███████| 20/20 [00:22<00:00, 1.11s/it]
Plot the trained KAN
model.plot(beta=10)
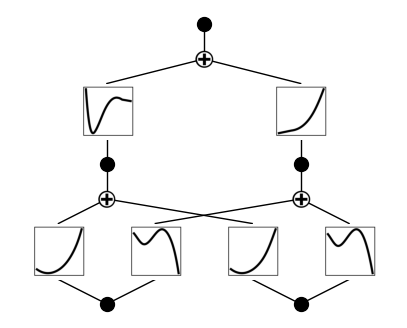
Fix the first layer activation to be linear function, and the second layer to be sine functions (caveat: this is quite sensitive to hypreparams)
model.fix_symbolic(0,0,0,'x')
model.fix_symbolic(0,0,1,'x')
model.fix_symbolic(0,1,0,'x')
model.fix_symbolic(0,1,1,'x')
r2 is 0.8357976675033569
r2 is not very high, please double check if you are choosing the correct symbolic function.
saving model version 0.1
r2 is 0.8300805687904358
r2 is not very high, please double check if you are choosing the correct symbolic function.
saving model version 0.2
r2 is 0.8376883268356323
r2 is not very high, please double check if you are choosing the correct symbolic function.
saving model version 0.3
r2 is 0.8372848629951477
r2 is not very high, please double check if you are choosing the correct symbolic function.
saving model version 0.4
tensor(0.8373)
After setting all to be symbolic, we further train the model (affine parameters are still trainable). The model can now reach machine precision!
train()
pde loss: 1.71e+01 | bc loss: 1.14e-02 | l2: 1.37e-01 : 50%|███▌ | 10/20 [00:11<00:11, 1.20s/it]
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
/var/folders/6j/b6y80djd4nb5hl73rv3sv8y80000gn/T/ipykernel_75424/3364925475.py in <module>
----> 1 train()
/var/folders/6j/b6y80djd4nb5hl73rv3sv8y80000gn/T/ipykernel_75424/2545871995.py in train()
76 model.update_grid_from_samples(x_i)
77
---> 78 optimizer.step(closure)
79 sol = sol_fun(x_i)
80 loss = alpha * pde_loss + bc_loss
~/opt/anaconda3/lib/python3.9/site-packages/torch/optim/optimizer.py in wrapper(*args, **kwargs)
383 )
384
--> 385 out = func(*args, **kwargs)
386 self._optimizer_step_code()
387
~/opt/anaconda3/lib/python3.9/site-packages/torch/utils/_contextlib.py in decorate_context(*args, **kwargs)
113 def decorate_context(*args, **kwargs):
114 with ctx_factory():
--> 115 return func(*args, **kwargs)
116
117 return decorate_context
~/Desktop/2022/research/code/pykan/kan/LBFGS.py in step(self, closure)
441 def obj_func(x, t, d):
442 return self._directional_evaluate(closure, x, t, d)
--> 443 loss, flat_grad, t, ls_func_evals = _strong_wolfe(
444 obj_func, x_init, t, d, loss, flat_grad, gtd)
445 self._add_grad(t, d)
~/Desktop/2022/research/code/pykan/kan/LBFGS.py in _strong_wolfe(obj_func, x, t, d, f, g, gtd, c1, c2, tolerance_change, max_ls)
48 g = g.clone(memory_format=torch.contiguous_format)
49 # evaluate objective and gradient using initial step
---> 50 f_new, g_new = obj_func(x, t, d)
51 ls_func_evals = 1
52 gtd_new = g_new.dot(d)
~/Desktop/2022/research/code/pykan/kan/LBFGS.py in obj_func(x, t, d)
440
441 def obj_func(x, t, d):
--> 442 return self._directional_evaluate(closure, x, t, d)
443 loss, flat_grad, t, ls_func_evals = _strong_wolfe(
444 obj_func, x_init, t, d, loss, flat_grad, gtd)
~/Desktop/2022/research/code/pykan/kan/LBFGS.py in _directional_evaluate(self, closure, x, t, d)
289 def _directional_evaluate(self, closure, x, t, d):
290 self._add_grad(t, d)
--> 291 loss = float(closure())
292 flat_grad = self._gather_flat_grad()
293 self._set_param(x)
~/opt/anaconda3/lib/python3.9/site-packages/torch/utils/_contextlib.py in decorate_context(*args, **kwargs)
113 def decorate_context(*args, **kwargs):
114 with ctx_factory():
--> 115 return func(*args, **kwargs)
116
117 return decorate_context
/var/folders/6j/b6y80djd4nb5hl73rv3sv8y80000gn/T/ipykernel_75424/2545871995.py in closure()
70
71 loss = alpha * pde_loss + bc_loss
---> 72 loss.backward()
73 return loss
74
~/opt/anaconda3/lib/python3.9/site-packages/torch/_tensor.py in backward(self, gradient, retain_graph, create_graph, inputs)
520 inputs=inputs,
521 )
--> 522 torch.autograd.backward(
523 self, gradient, retain_graph, create_graph, inputs=inputs
524 )
~/opt/anaconda3/lib/python3.9/site-packages/torch/autograd/__init__.py in backward(tensors, grad_tensors, retain_graph, create_graph, grad_variables, inputs)
264 # some Python versions print out the first line of a multi-line function
265 # calls in the traceback and some print out the last line
--> 266 Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward pass
267 tensors,
268 grad_tensors_,
KeyboardInterrupt:
Print out the symbolic formula
formula = model.symbolic_formula()[0][0]
ex_round(formula,6)
\[\displaystyle - 0.5 \sin{\left(3.141592 x_{1} + 3.141593 x_{2} - 4.712389 \right)} + 0.5 \sin{\left(3.141593 x_{1} - 3.141592 x_{2} + 1.570797 \right)}\]