Example 5: Special functions
Let’s construct a dataset which contains special functions \(f(x,y)={\rm exp}(J_0(20x)+y^2)\), where \(J_0(x)\) is the Bessel function.
from kan import *
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)
# create a KAN: 2D inputs, 1D output, and 5 hidden neurons. cubic spline (k=3), 5 grid intervals (grid=5).
model = KAN(width=[2,1,1], grid=3, k=3, seed=2, device=device)
f = lambda x: torch.exp(torch.special.bessel_j0(20*x[:,[0]]) + x[:,[1]]**2)
dataset = create_dataset(f, n_var=2, device=device)
# train the model
model.fit(dataset, opt="LBFGS", steps=20);
cuda
checkpoint directory created: ./model
saving model version 0.0
| train_loss: 5.15e-01 | test_loss: 5.86e-01 | reg: 5.84e+00 | : 100%|█| 20/20 [00:03<00:00, 5.89it
saving model version 0.1
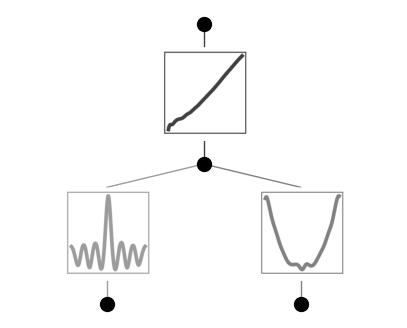
Plot trained KAN, the bessel function shows up in the bettom left
model.plot()
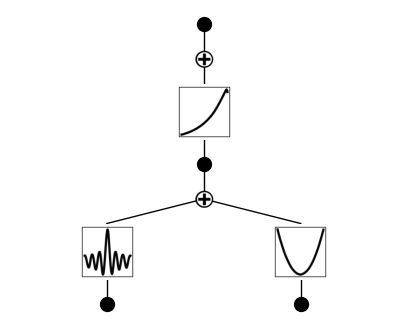
model = model.refine(20)
model.fit(dataset, opt="LBFGS", steps=20);
saving model version 0.2
| train_loss: 1.54e-02 | test_loss: 4.73e-02 | reg: 7.50e+00 | : 100%|█| 20/20 [00:02<00:00, 6.93it
saving model version 0.3
model.plot()
suggest_symbolic does not return anything that matches with it, since Bessel function isn’t included in the default SYMBOLIC_LIB. We want to add Bessel to it.
model.suggest_symbolic(0,0,0)
function fitting r2 r2 loss complexity complexity loss total loss
0 0 0.000000 0.000014 0 0 0.000003
1 x 0.001602 -0.002298 1 1 0.799540
2 sin 0.161428 -0.253977 2 2 1.549205
3 cos 0.161428 -0.253977 2 2 1.549205
4 1/x^2 0.099456 -0.151116 2 2 1.569777
('0',
(<function kan.utils.<lambda>(x)>,
<function kan.utils.<lambda>(x)>,
0,
<function kan.utils.<lambda>(x, y_th)>),
0.0,
0)
SYMBOLIC_LIB.keys()
dict_keys(['x', 'x^2', 'x^3', 'x^4', 'x^5', '1/x', '1/x^2', '1/x^3', '1/x^4', '1/x^5', 'sqrt', 'x^0.5', 'x^1.5', '1/sqrt(x)', '1/x^0.5', 'exp', 'log', 'abs', 'sin', 'cos', 'tan', 'tanh', 'sgn', 'arcsin', 'arccos', 'arctan', 'arctanh', '0', 'gaussian'])
add bessel function J0 to the symbolic library. we should include a name and a pytorch implementation. c is the complexity assigned to J0.
add_symbolic('J0', torch.special.bessel_j0, c=1)
After adding Bessel, we check suggest_symbolic again
# J0 fitting is not very good
model.suggest_symbolic(0,0,0)
function fitting r2 r2 loss complexity complexity loss total loss
0 0 0.000000 0.000014 0 0 0.000003
1 J0 0.198505 -0.319216 1 1 0.736157
2 x 0.001602 -0.002298 1 1 0.799540
3 sin 0.161428 -0.253977 2 2 1.549205
4 cos 0.161428 -0.253977 2 2 1.549205
('0',
(<function kan.utils.<lambda>(x)>,
<function kan.utils.<lambda>(x)>,
0,
<function kan.utils.<lambda>(x, y_th)>),
0.0,
0)
The fitting r2 is still not high, this is because the ground truth is J0(20x) which involves 20 which is too large. our default search is in (-10,10). so we need to set the search range bigger in order to include 20. now J0 appears at the top of the list
model.suggest_symbolic(0,0,0,a_range=(-40,40))
function fitting r2 r2 loss complexity complexity loss total loss
0 J0 0.998912 -9.830484 1 1 -1.166097
1 0 0.000000 0.000014 0 0 0.000003
2 x 0.001602 -0.002298 1 1 0.799540
3 cos 0.583964 -1.265186 2 2 1.346963
4 sin 0.583964 -1.265186 2 2 1.346963
('J0',
(<function torch._C._special.special_bessel_j0>,
J0,
1,
<function torch._C._special.special_bessel_j0>),
0.9989116787910461,
1)