Example 12: Unsupervised learning

In this example, we will use KAN for unsupervised learning. Instead of trying to figure out how a target variable \(y\) depends on input variables, we treat all variables on the equal footing (as input variables). Below we contruct a synthetic dataset where we have six variables \(x_1, x_2, x_3, x_4, x_5, x_6\). \((x_1, x_2, x_3)\) are dependent such that \(x_3={\rm exp}({\rm sin}(\pi x_1)+x_2^2)\); \((x_4,x_5)\) are dependent such that \(x_5=x_4^3\). And \(x_6\) is independent of all other variables. Can we use KANs to discover these dependent groups?

The idea is that we treat the problem as a classification problem. The dataset that satisfies these interdependent relations are ‘positive’ samples, while corrupted samples (by random permutation of features across samples) are ‘negative’ samples. We want to train a KAN to output 1 when it is a positive sample, and output 0 when it is a negative sample. We set the last layer activation to be Gaussian, so positive samples will have zero activation in the second to last layer, while negtive samples will have non-zero activation in the second to last layer. We can then define the relation implicitly as \(g=0\) where \(g\) is the activation in the second to last layer.

Intialize model and create dataset

from kan import KAN
import torch
import copy

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)

seed = 1

model = KAN(width=[6,1,1], grid=3, k=3, seed=seed, device=device)

# create dataset


def create_dataset(train_num=500, test_num=500):

    def generate_contrastive(x):
        # positive samples
        batch = x.shape[0]
        x[:,2] = torch.exp(torch.sin(torch.pi*x[:,0])+x[:,1]**2)
        x[:,3] = x[:,4]**3

        # negative samples
        def corrupt(tensor):
            y = copy.deepcopy(tensor)
            for i in range(y.shape[1]):
                y[:,i] = y[:,i][torch.randperm(y.shape[0])]
            return y

        x_cor = corrupt(x)
        x = torch.cat([x, x_cor], dim=0)
        y = torch.cat([torch.ones(batch,), torch.zeros(batch,)], dim=0)[:,None]
        return x, y

    x = torch.rand(train_num, 6) * 2 - 1
    x_train, y_train = generate_contrastive(x)

    x = torch.rand(test_num, 6) * 2 - 1
    x_test, y_test = generate_contrastive(x)

    dataset = {}
    dataset['train_input'] = x_train.to(device)
    dataset['test_input'] = x_test.to(device)
    dataset['train_label'] = y_train.to(device)
    dataset['test_label'] = y_test.to(device)
    return dataset

dataset = create_dataset()

cuda
checkpoint directory created: ./model
saving model version 0.0

model(dataset['train_input'])
model.plot(beta=10)

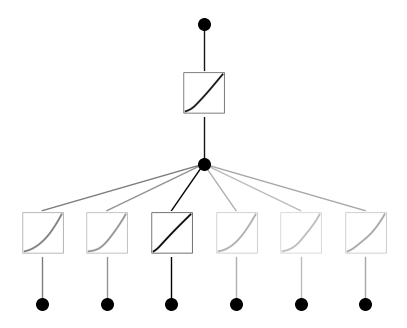
# set the (1,0,0) activation to be gausssian
#model.fix_symbolic(1,0,0,lambda x: torch.exp(-x**2/10),fit_params_bool=False)
model.fix_symbolic(1,0,0,'gaussian',fit_params_bool=False)

saving model version 0.1

model(dataset['train_input'])
model.plot(beta=10)

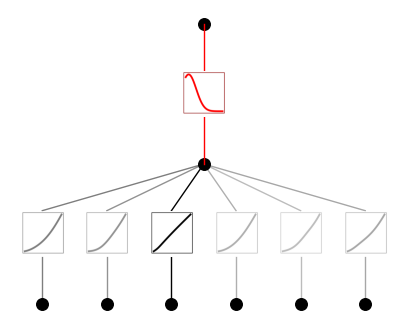
model.fit(dataset, opt="LBFGS", steps=50, lamb=0.002, lamb_entropy=10.0, lamb_coef=1.0);

| train_loss: 1.80e-01 | test_loss: 1.78e-01 | reg: 3.77e+01 | : 100%|█| 50/50 [00:13<00:00,  3.76it

saving model version 0.2

model.plot(in_vars=[r'$x_{}$'.format(i) for i in range(1,7)])

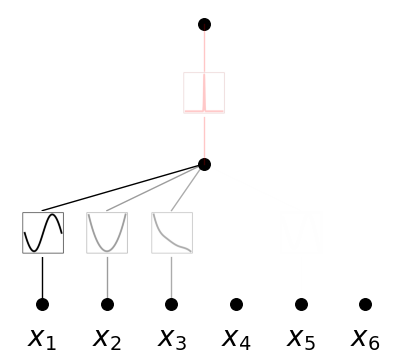
This gives the dependence among \((x_4,x_5)\). Another random seed can give dependence among \((x_1,x_2,x_3)\).