Hello, KAN!

Kolmogorov-Arnold representation theorem

Kolmogorov-Arnold representation theorem states that if \(f\) is a multivariate continuous function on a bounded domain, then it can be written as a finite composition of continuous functions of a single variable and the binary operation of addition. More specifically, for a smooth \(f : [0,1]^n \to \mathbb{R}\),

\[f(x) = f(x_1,...,x_n)=\sum_{q=1}^{2n+1}\Phi_q(\sum_{p=1}^n \phi_{q,p}(x_p))\]

where \(\phi_{q,p}:[0,1]\to\mathbb{R}\) and \(\Phi_q:\mathbb{R}\to\mathbb{R}\). In a sense, they showed that the only true multivariate function is addition, since every other function can be written using univariate functions and sum. However, this 2-Layer width-\((2n+1)\) Kolmogorov-Arnold representation may not be smooth due to its limited expressive power. We augment its expressive power by generalizing it to arbitrary depths and widths.

Kolmogorov-Arnold Network (KAN)

The Kolmogorov-Arnold representation can be written in matrix form

\[f(x)={\bf \Phi}_{\rm out}\circ{\bf \Phi}_{\rm in}\circ {\bf x}\]

where

\[\begin{split}{\bf \Phi}_{\rm in}= \begin{pmatrix} \phi_{1,1}(\cdot) & \cdots & \phi_{1,n}(\cdot) \\ \vdots & & \vdots \\ \phi_{2n+1,1}(\cdot) & \cdots & \phi_{2n+1,n}(\cdot) \end{pmatrix},\quad {\bf \Phi}_{\rm out}=\begin{pmatrix} \Phi_1(\cdot) & \cdots & \Phi_{2n+1}(\cdot)\end{pmatrix}\end{split}\]

We notice that both \({\bf \Phi}_{\rm in}\) and \({\bf \Phi}_{\rm out}\) are special cases of the following function matrix \({\bf \Phi}\) (with \(n_{\rm in}\) inputs, and \(n_{\rm out}\) outputs), we call a Kolmogorov-Arnold layer:

\[\begin{split}{\bf \Phi}= \begin{pmatrix} \phi_{1,1}(\cdot) & \cdots & \phi_{1,n_{\rm in}}(\cdot) \\ \vdots & & \vdots \\ \phi_{n_{\rm out},1}(\cdot) & \cdots & \phi_{n_{\rm out},n_{\rm in}}(\cdot) \end{pmatrix}\end{split}\]

\({\bf \Phi}_{\rm in}\) corresponds to \(n_{\rm in}=n, n_{\rm out}=2n+1\), and \({\bf \Phi}_{\rm out}\) corresponds to \(n_{\rm in}=2n+1, n_{\rm out}=1\).

After defining the layer, we can construct a Kolmogorov-Arnold network simply by stacking layers! Let’s say we have \(L\) layers, with the \(l^{\rm th}\) layer \({\bf \Phi}_l\) have shape \((n_{l+1}, n_{l})\). Then the whole network is

\[{\rm KAN}({\bf x})={\bf \Phi}_{L-1}\circ\cdots \circ{\bf \Phi}_1\circ{\bf \Phi}_0\circ {\bf x}\]

In constrast, a Multi-Layer Perceptron is interleaved by linear layers \({\bf W}_l\) and nonlinearities \(\sigma\):

\[{\rm MLP}({\bf x})={\bf W}_{L-1}\circ\sigma\circ\cdots\circ {\bf W}_1\circ\sigma\circ {\bf W}_0\circ {\bf x}\]

A KAN can be easily visualized. (1) A KAN is simply stack of KAN layers. (2) Each KAN layer can be visualized as a fully-connected layer, with a 1D function placed on each edge. Let’s see an example below.

Get started with KANs

Initialize KAN

from kan import *
# create a KAN: 2D inputs, 1D output, and 5 hidden neurons. cubic spline (k=3), 5 grid intervals (grid=5).
model = KAN(width=[2,5,1], grid=5, k=3, seed=0)

Create dataset

# create dataset f(x,y) = exp(sin(pi*x)+y^2)
f = lambda x: torch.exp(torch.sin(torch.pi*x[:,[0]]) + x[:,[1]]**2)
dataset = create_dataset(f, n_var=2)
dataset['train_input'].shape, dataset['train_label'].shape

(torch.Size([1000, 2]), torch.Size([1000, 1]))

Plot KAN at initialization

# plot KAN at initialization
model(dataset['train_input']);
model.plot(beta=100)
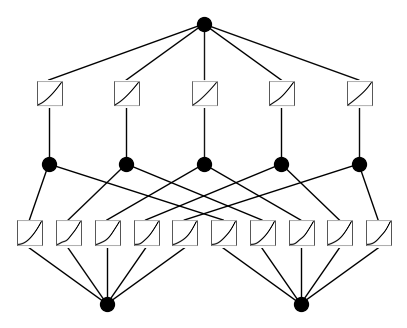
_images/intro_15_0.png

Train KAN with sparsity regularization

# train the model
model.train(dataset, opt="LBFGS", steps=20, lamb=0.01, lamb_entropy=10.);

train loss: 1.57e-01 | test loss: 1.31e-01 | reg: 2.05e+01 : 100%|██| 20/20 [00:18<00:00,  1.06it/s]

Plot trained KAN

model.plot()
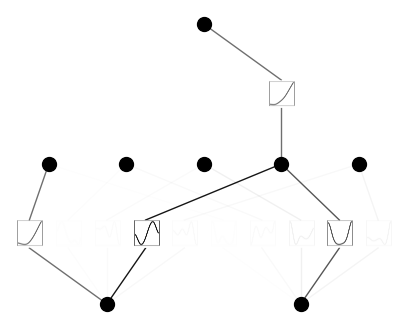
_images/intro_19_0.png

Prune KAN and replot (keep the original shape)

model.prune()
model.plot(mask=True)
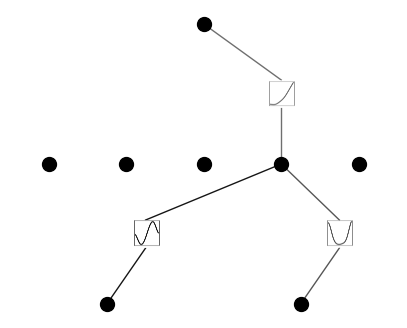
_images/intro_21_0.png

Prune KAN and replot (get a smaller shape)

model = model.prune()
model(dataset['train_input'])
model.plot()
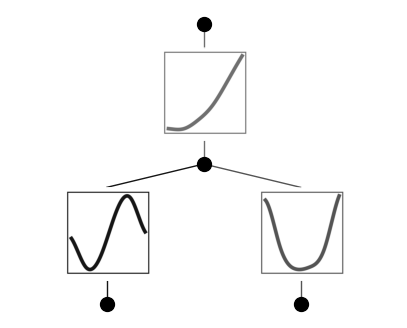
_images/intro_23_0.png

Continue training and replot

model.train(dataset, opt="LBFGS", steps=50);

train loss: 4.74e-03 | test loss: 4.80e-03 | reg: 2.98e+00 : 100%|██| 50/50 [00:07<00:00,  7.03it/s]

model.plot()
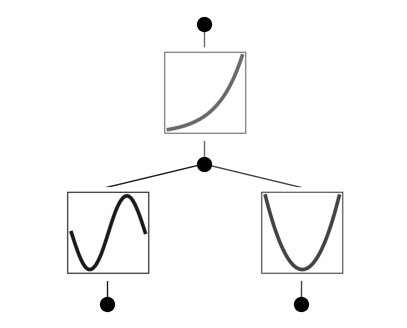
_images/intro_26_0.png

Automatically or manually set activation functions to be symbolic

mode = "auto" # "manual"

if mode == "manual":
    # manual mode
    model.fix_symbolic(0,0,0,'sin');
    model.fix_symbolic(0,1,0,'x^2');
    model.fix_symbolic(1,0,0,'exp');
elif mode == "auto":
    # automatic mode
    lib = ['x','x^2','x^3','x^4','exp','log','sqrt','tanh','sin','abs']
    model.auto_symbolic(lib=lib)

fixing (0,0,0) with sin, r2=0.999987252534279
fixing (0,1,0) with x^2, r2=0.9999996536741071
fixing (1,0,0) with exp, r2=0.9999988529417926

Continue training to almost machine precision

model.train(dataset, opt="LBFGS", steps=50);

train loss: 2.02e-10 | test loss: 1.13e-10 | reg: 2.98e+00 : 100%|██| 50/50 [00:02<00:00, 22.59it/s]

Obtain the symbolic formula

model.symbolic_formula()[0][0]
\[\displaystyle 1.0 e^{1.0 x_{2}^{2} + 1.0 \sin{\left(3.14 x_{1} \right)}}\]