Physics 1: Lagrangian neural network
from kan import *
from kan.utils import batch_jacobian, batch_hessian
torch.use_deterministic_algorithms(True)
torch.set_default_dtype(torch.float64)
seed = 0
torch.manual_seed(seed)
#example = 'harmonic_oscillator'
#example = 'single_pendulum'
example = 'relativistic_mass'
# three examples: harmonic oscillator, single pendulum, double pendulum
# dimension of q
# Lagrangian: (q, qd) -> (qdd)
if example == 'harmonic_oscillator':
n_sample = 1000
# harmonic oscillator
d = 1
q = torch.rand(size=(n_sample,1)) * 4 - 2
qd = torch.rand(size=(n_sample,1)) * 4 - 2
qdd = - q
x = torch.cat([q, qd], dim=1)
if example == 'single_pendulum':
n_sample = 1000
# harmonic oscillator
d = 1
q = torch.rand(size=(n_sample,1)) * 4 - 2
qd = torch.rand(size=(n_sample,1)) * 4 - 2
qdd = - torch.sin(q)
x = torch.cat([q, qd], dim=1)
if example == 'relativistic_mass':
n_sample = 10000
# harmonic oscillator
d = 1
q = torch.rand(size=(n_sample,1)) * 4 - 2
#qd = torch.rand(size=(n_sample,1)) * 1.998 - 0.999
#qd = 0.95 + torch.rand(size=(n_sample,1)) * 0.05
qd = torch.rand(size=(n_sample,1)) * 2 - 1
qdd = (1 - qd**2)**(3/2)
x = torch.cat([q, qd], dim=1)
from kan.compiler import kanpiler
from sympy import *
input_variables = symbol_x, symbol_vx = symbols('x v_x')
expr = symbol_vx ** 2
model = kanpiler(input_variables, expr, grid=20)
saving model version 0.1
model.get_act(x)
model.plot()
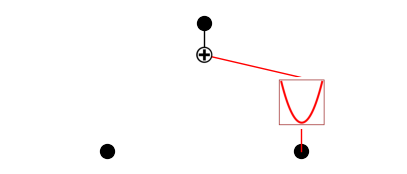
model.perturb(mode='best', mag=0.1)
model.get_act(x)
model.plot()
saving model version 0.2
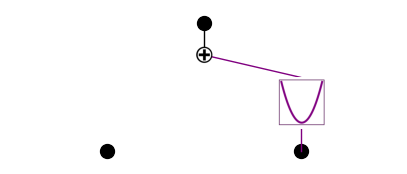
from kan import *
from kan.utils import batch_jacobian, create_dataset_from_data
import numpy as np
torch.use_deterministic_algorithms(True)
def closure():
global loss
optimizer.zero_grad()
jacobian = batch_jacobian(model, x, create_graph=True)
hessian = batch_hessian(model, x, create_graph=True)
Lqdqd = hessian[:,d:,d:]
Lq = jacobian[:,:d]
Lqqd = hessian[:,d:,:d]
Lqqd_qd_prod = torch.einsum('ijk,ik->ij', Lqqd, qd)
qdd_pred = torch.einsum('ijk,ik->ij', torch.linalg.inv(Lqdqd), Lq - Lqqd_qd_prod)
loss = torch.mean((qdd - qdd_pred)**2)
loss.backward()
return loss
steps = 20
log = 1
optimizer = LBFGS(model.parameters(), lr=1, history_size=10, line_search_fn="strong_wolfe", tolerance_grad=1e-32, tolerance_change=1e-32, tolerance_ys=1e-32)
#optimizer = torch.optim.Adam(params, lr=1e-2)
pbar = tqdm(range(steps), desc='description', ncols=100)
for _ in pbar:
# update grid
if _ < 5 and _ % 20 == 0:
model.update_grid(x)
optimizer.step(closure)
if _ % log == 0:
pbar.set_description("| loss: %.2e |" % loss.cpu().detach().numpy())
| loss: 5.03e-05 |: 100%|███████████████████████████████████████████| 20/20 [02:59<00:00, 8.99s/it]
model.plot()
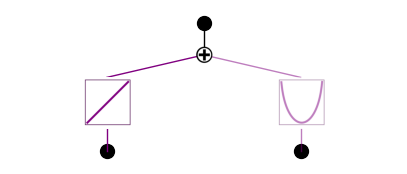
model.auto_symbolic()
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
/var/folders/6j/b6y80djd4nb5hl73rv3sv8y80000gn/T/ipykernel_24271/2849209031.py in <module>
----> 1 model.auto_symbolic()
~/Desktop/2022/research/code/pykan/kan/MultKAN.py in auto_symbolic(self, a_range, b_range, lib, verbose)
1402 print(f'fixing ({l},{i},{j}) with 0')
1403 else:
-> 1404 name, fun, r2, c = self.suggest_symbolic(l, i, j, a_range=a_range, b_range=b_range, lib=lib, verbose=False)
1405 self.fix_symbolic(l, i, j, name, verbose=verbose > 1, log_history=False)
1406 if verbose >= 1:
~/Desktop/2022/research/code/pykan/kan/MultKAN.py in suggest_symbolic(self, l, i, j, a_range, b_range, lib, topk, verbose, r2_loss_fun, c_loss_fun, weight_simple)
1332 # getting r2 and complexities
1333 for (name, content) in symbolic_lib.items():
-> 1334 r2 = self.fix_symbolic(l, i, j, name, a_range=a_range, b_range=b_range, verbose=False, log_history=False)
1335 if r2 == -1e8: # zero function
1336 r2s.append(-1e8)
~/Desktop/2022/research/code/pykan/kan/MultKAN.py in fix_symbolic(self, l, i, j, fun_name, fit_params_bool, a_range, b_range, verbose, random, log_history)
488 y = self.spline_postacts[l][:, j, i]
489 #y = self.postacts[l][:, j, i]
--> 490 r2 = self.symbolic_fun[l].fix_symbolic(i, j, fun_name, x, y, a_range=a_range, b_range=b_range, verbose=verbose)
491 if mask[i,j] == 0:
492 r2 = - 1e8
~/Desktop/2022/research/code/pykan/kan/Symbolic_KANLayer.py in fix_symbolic(self, i, j, fun_name, x, y, random, a_range, b_range, verbose)
229 else:
230 #initialize from x & y and fun
--> 231 params, r2 = fit_params(x,y,fun, a_range=a_range, b_range=b_range, verbose=verbose, device=self.device)
232 self.funs[j][i] = fun
233 self.funs_avoid_singularity[j][i] = fun_avoid_singularity
~/Desktop/2022/research/code/pykan/kan/utils.py in fit_params(x, y, fun, a_range, b_range, grid_number, iteration, verbose, device)
235 b_ = torch.linspace(b_range[0], b_range[1], steps=grid_number, device=device)
236 a_grid, b_grid = torch.meshgrid(a_, b_, indexing='ij')
--> 237 post_fun = fun(a_grid[None,:,:] * x[:,None,None] + b_grid[None,:,:])
238 x_mean = torch.mean(post_fun, dim=[0], keepdim=True)
239 y_mean = torch.mean(y, dim=[0], keepdim=True)
KeyboardInterrupt:
model.unfix_symbolic(0,0,0)
model.suggest_symbolic(0,0,0)
saving model version 0.5
function fitting r2 r2 loss complexity complexity loss total loss
0 x 1.000000 -16.565706 1 1 -2.513141
1 cos 1.000000 -16.599499 2 2 -1.719900
2 sin 1.000000 -16.599499 2 2 -1.719900
3 exp 0.999997 -16.268112 2 2 -1.653622
4 x^0.5 0.999977 -14.896568 2 2 -1.379314
('x',
(<function kan.utils.<lambda>(x)>,
<function kan.utils.<lambda>(x)>,
1,
<function kan.utils.<lambda>(x, y_th)>),
0.9999996907837526,
1)
model.unfix_symbolic(0,1,0)
model.suggest_symbolic(0,1,0)
saving model version 0.4
function fitting r2 r2 loss complexity complexity loss total loss
0 0 0.000000 0.000014 0 0 0.000003
1 cos 0.969503 -5.034727 2 2 0.593055
2 x^2 0.969092 -5.015413 2 2 0.596917
3 sin 0.965249 -4.846400 2 2 0.630720
4 x 0.000392 -0.000551 1 1 0.799890
('0',
(<function kan.utils.<lambda>(x)>,
<function kan.utils.<lambda>(x)>,
0,
<function kan.utils.<lambda>(x, y_th)>),
0.0,
0)
x, y = model.get_fun(0,1,0)
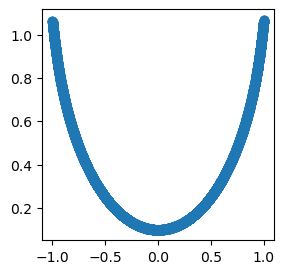
from kan.utils import create_dataset_from_data
dataset2 = create_dataset_from_data(x[:,None], y[:,None])
model2 = KAN(width=[1,1,1])
model2.fix_symbolic(0,0,0,'x^2',fit_params_bool=False)
checkpoint directory created: ./model
saving model version 0.0
saving model version 0.1
model2.get_act(dataset2)
model2.plot()
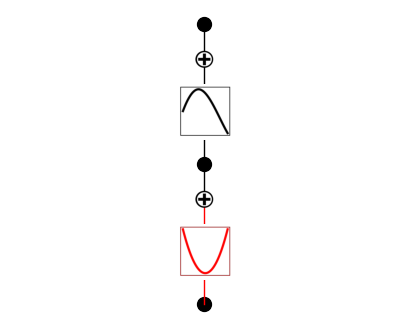
model2.fit(dataset2, steps=50);
| train_loss: 3.77e-04 | test_loss: 3.76e-04 | reg: 3.35e+00 | : 100%|█| 50/50 [00:46<00:00, 1.07it
saving model version 0.2
model2.fit(dataset2, steps=50, update_grid=False);
| train_loss: 3.73e-04 | test_loss: 3.72e-04 | reg: 3.35e+00 | : 100%|█| 50/50 [00:13<00:00, 3.81it
saving model version 0.3
model2.plot()
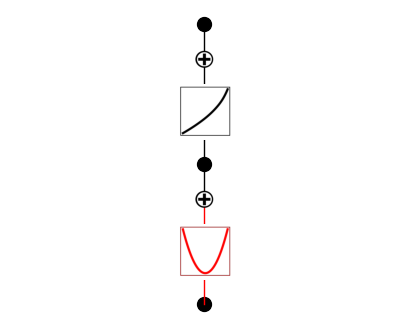
model2.suggest_symbolic(1,0,0)
function fitting r2 r2 loss complexity complexity loss total loss
0 x^0.5 0.999957 -14.193489 2 2 -1.238698
1 sqrt 0.999957 -14.193489 2 2 -1.238698
2 log 0.999722 -11.763921 2 2 -0.752784
3 1/x^0.5 0.999485 -10.894391 2 2 -0.578878
4 1/sqrt(x) 0.999485 -10.894391 2 2 -0.578878
('x^0.5',
(<function kan.utils.<lambda>(x)>,
<function kan.utils.<lambda>(x)>,
2,
<function kan.utils.<lambda>(x, y_th)>),
0.9999566254728288,
2)
from kan.utils import fit_params
fit_params(x**2, y, lambda x: x**(1/2))
Best value at boundary.
r2 is 0.9989821969546337
(tensor([-9.8000, 9.8868, -0.3482, 1.2049]), tensor(0.9990))
model2.auto_symbolic()
skipping (0,0,0) since already symbolic
fixing (1,0,0) with x^0.5, r2=0.9999494098870415, c=2
saving model version 0.4
from kan.utils import ex_round
ex_round(model2.symbolic_formula()[0][0], 2)
\[\displaystyle 1.19 - 1.08 \sqrt{1 - 1.0 x_{1}^{2}}\]