Bayesian learning
Bayesian Learning
Bayesian models are more robust.
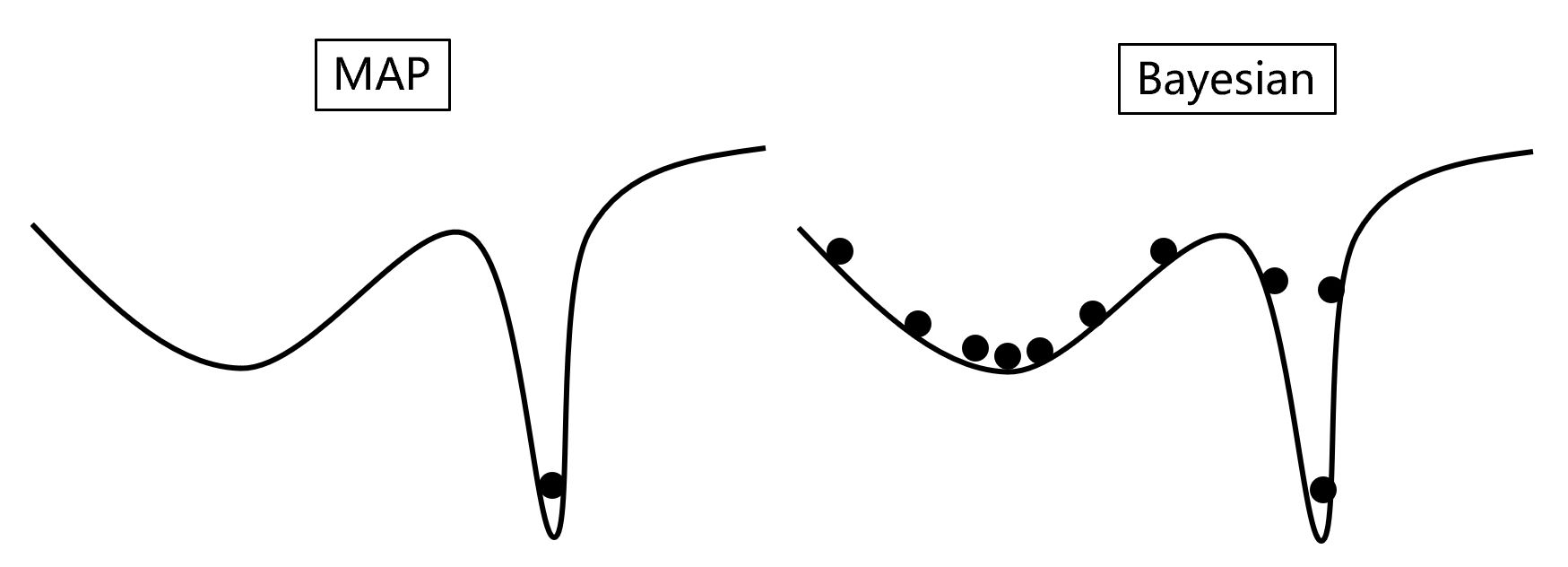
Why do we need Bayesian models? For machine learning models, over-fitting is a problem that can produce bad generalization. To illustrate the point, let us consider a loss function composed of a shallow wide well and a deep thin well. It is believed that the deep well, although with lower loss function, possibly has worse generalization compared to the shallow one. With Maximum A posterior Estimation (Or simply optimization of the loss function), there is larger chance we reach the deap well.
However with bayesian learning, the obtained sample density is dependent on both the loss function, and the volume of the phase space. As a result, more samples will fall into the shallow but wide well, meaning we have larger chance to obtain a model with fair robustness. Furthermore, uncertainties are available in the framework of bayesian learning, unlike optimization solvers.
Quantum-inspired Hamiltonian Monte Carlo
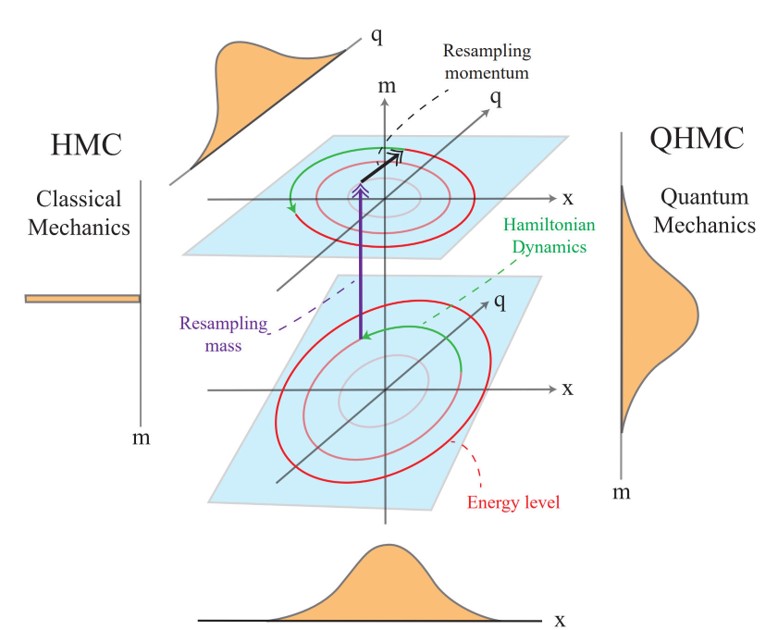
Inspired by quantum mechanics, we modify the Hamiltonian Monte Carlo integrators by introducing a time-varying mass term. We analyze the new sampler from the perspectives of dynamical systems and game theory. We demonstrate the effectiveness of the proposed method with applications in bayesian bridge regression, image denoising and neural network pruning.
The paper will appear on Arxiv soon.