Sparse attention 3 -- inefficiency of extracting similar content

Author: Ziming Liu (刘子鸣)

Motivation

In Sparse-attention-1, we showed that a single-layer attention model (without positional embeddings) can learn to copy the current token. In Sparse-attention-2, we showed that the same model is unable to extract a specific previous token based on position, e.g., the last token. But what about extracting a previous token based on content (semantic meaning)? This is a more natural task, because it is precisely what attention is designed to do—attend to similar content.

As we show below, somewhat surprisingly, a single attention layer is very inefficient at performing this extraction task.

Problem setup

Dataset
The task is to extract the token that is most similar to the current token. We assume tokens have numerical meanings; for example, token \([5]\) represents the number \(5\). Then \([5]\) is closer to \([6]\) than to \([8]\) because \(1=|5-6| < |5-8|=3.\)

Taking context length = 4 as an example, the task is to predict \([1][5][10][6] \rightarrow [5]\).
This is because \([5]\) is the closest to \([6]\), than \([1]\) or \([10]\).

Model
We stick to the toy model from the previous blog. The model consists only of an Embedding layer, an Unembedding layer, and a single Attention layer, with no MLP layers and no positional embeddings.

Failure even for context length = 3 (with small embedding dimension)

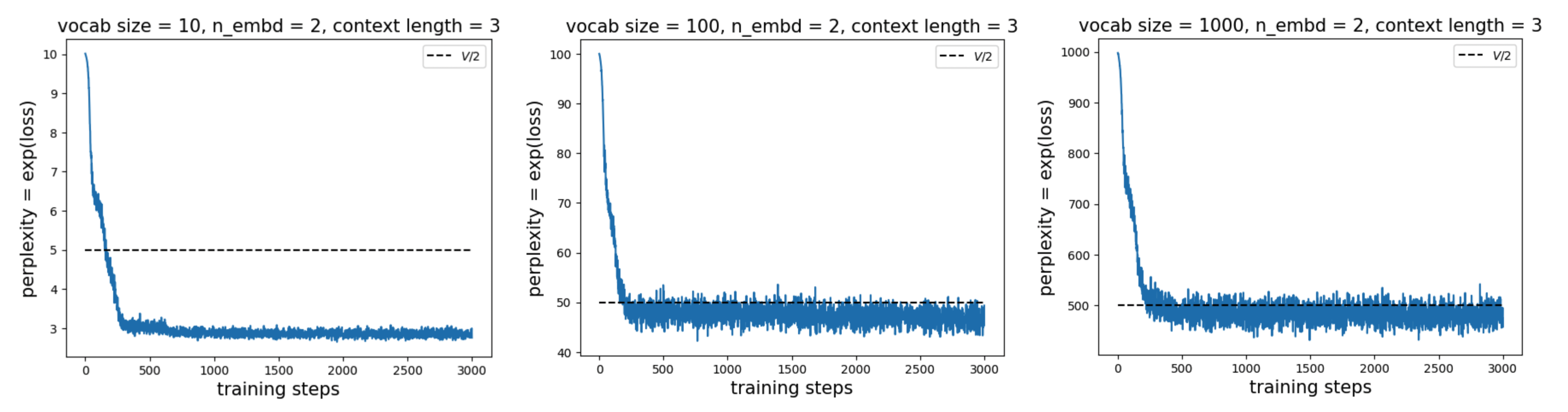
We examine the loss curves (in practice, we plot perplexity, i.e., \({\rm exp(loss)}\)). For embedding dimension = 2 and context length = 3 (task: \([1][5][6]\to[5]\)), as we vary the vocabulary size, we consistently observe that perplexity converges to \(V/2\) (or lower, for smaller \(V\)).

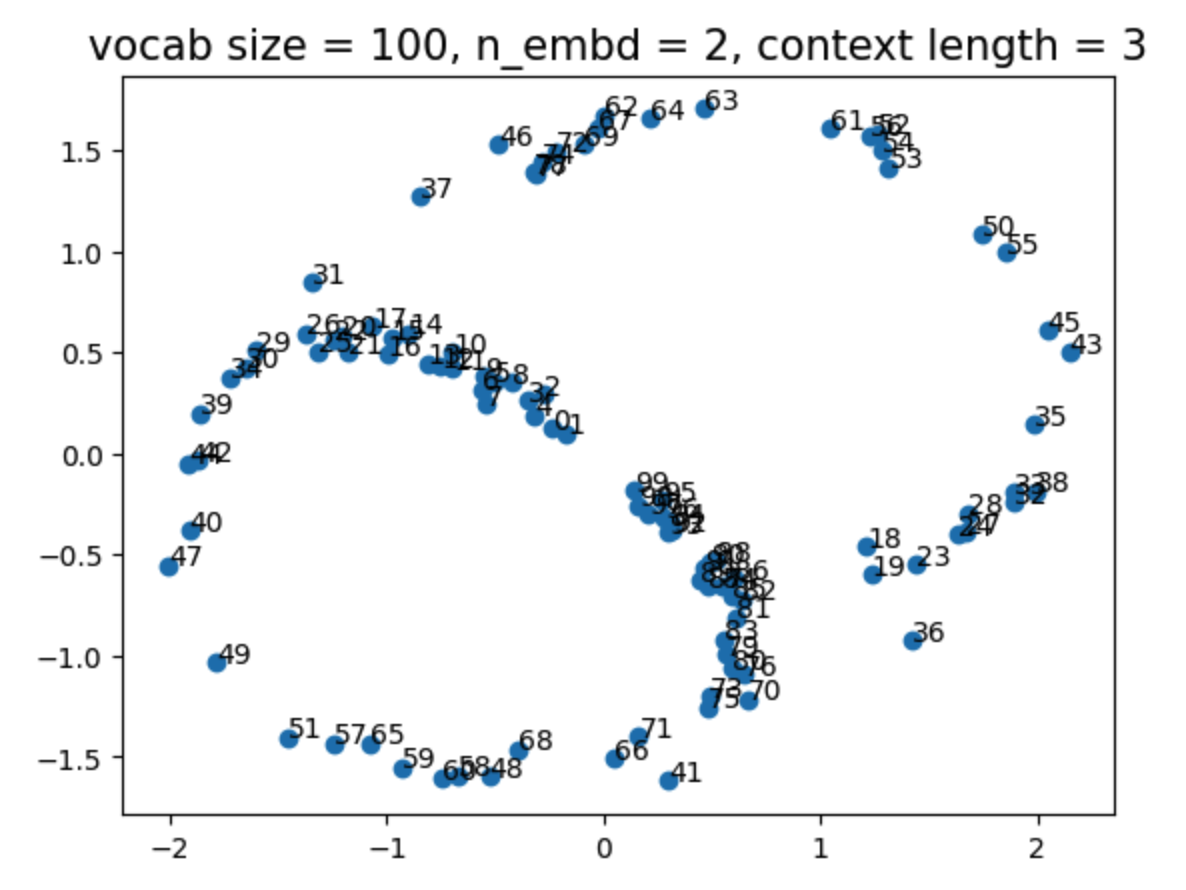
By visualizing the learned embeddings, we find that they exhibit a continuous structure; that is, numerically closer tokens are embedded closer together:

Dependence on vocab size \(V\)

The existence of structure may explain why the perplexity can fall slightly below \(V/2\): the continuous geometric structure is partially learned and leveraged to reduce the loss. However, the model largely becomes confused (similar to what we observed in the previous blog) and effectively guesses a random token from the previous context. This leads to a perplexity of \(\frac{C-2}{C-1}V\), which qualitatively (though not quantitatively) matches the experimental results:

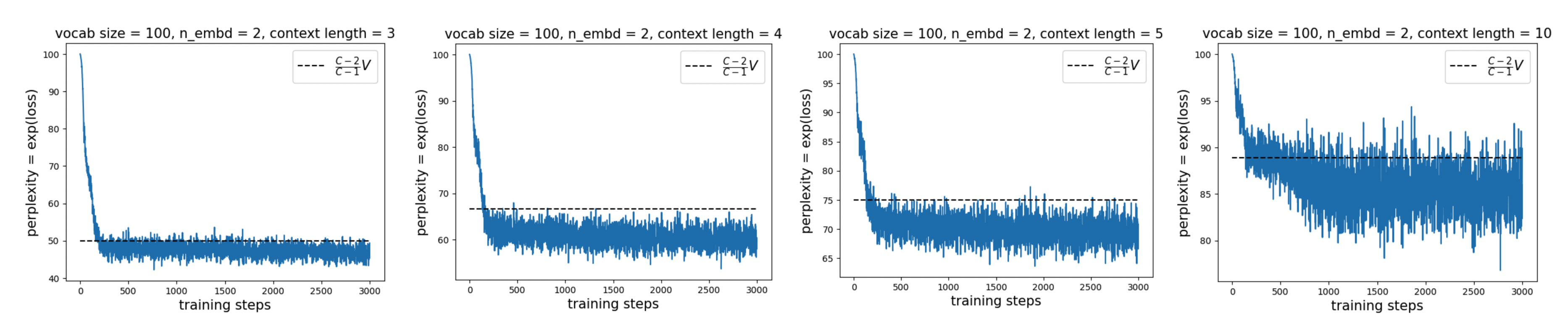
Dependence on embedding dimension

We find that the best achievable perplexity decreases with \(n_{\rm embd}\), in fact faster than \(V/n_{\rm embd}\):

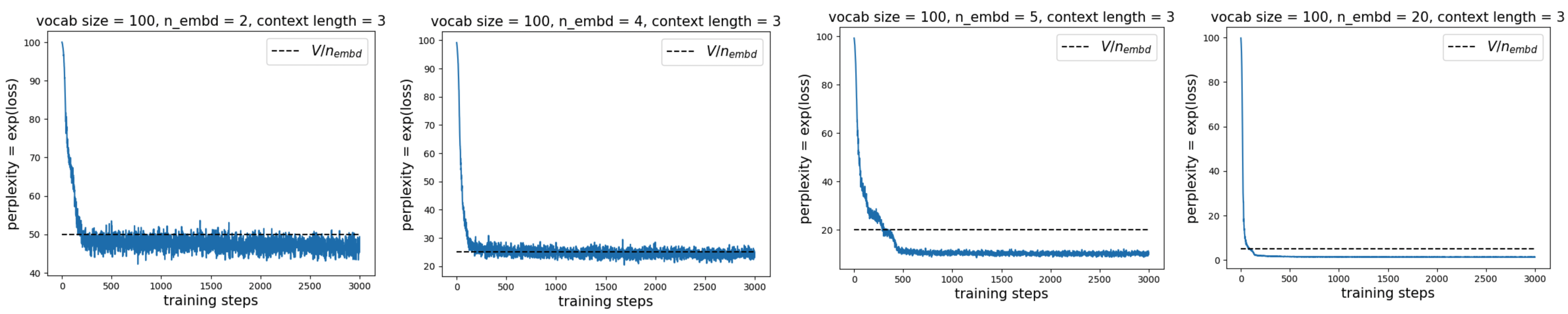
This may be explained by the increasingly improved geometry of the embeddings (as seen in the first two principal components) as we increase \(n_{\rm embd}\):

Questions / Ideas

• Our results demonstrate the ineffectiveness of attention in extracting similar content in this setting.
• One possible fix is to replace the inner product of Q/K with the Euclidean distance between Q and K. Ideally, a 1D embedding would already be sufficient if the kernel computes Euclidean distances and weighs probabilities inversely proportional to distance (similar to harmonic loss). The innner-product in attention probably produces the inefficiency, and we should try other distance measures.

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026sparse-attention-3,
  title={Sparse attention 3 -- inefficiency of extracting similar content},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/sparse-attention-3/}
}