Sparse attention 1 -- sticky plateau and rank collapse

Author: Ziming Liu (刘子鸣)

Motivation

The idea of attention is to select what we want from a collection of items. Token embeddings select based on content itself, while positional embeddings select based on position.

In this article, we examine attention’s ability to select based on content. Therefore, for simplicity, we ignore positional embeddings.

Problem setup

Dataset
The task is: select the current token. Taking context length = 4 as an example, this is
\([A][B][C][D] \rightarrow [D]\).

Model
The model consists of only Embedding, Unembedding, and a single Attention layer, with no MLP layers. The main tunable parameters are the vocabulary size, embedding dimension, and context length.

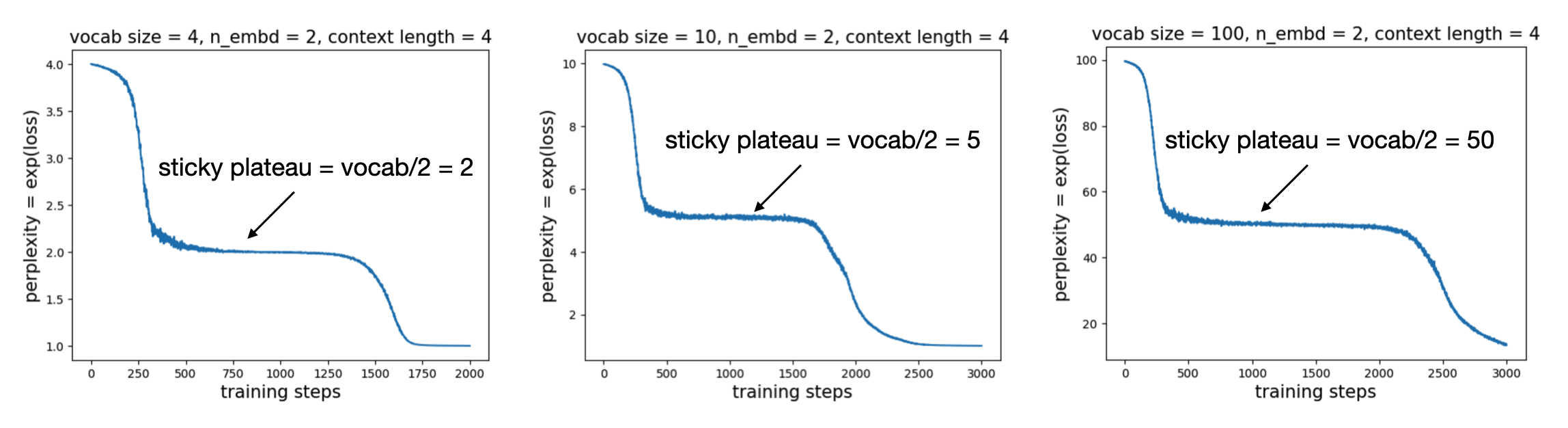
Observation: sticky plateau

We examine the loss curves (in practice, we plot perplexity, i.e. \({\rm exp(loss)}\)). For embedding dimension = 2 and context length = 4, as we vary the vocabulary size, we consistently observe a sticky plateau, where the perplexity corresponds to half of the vocabulary size.

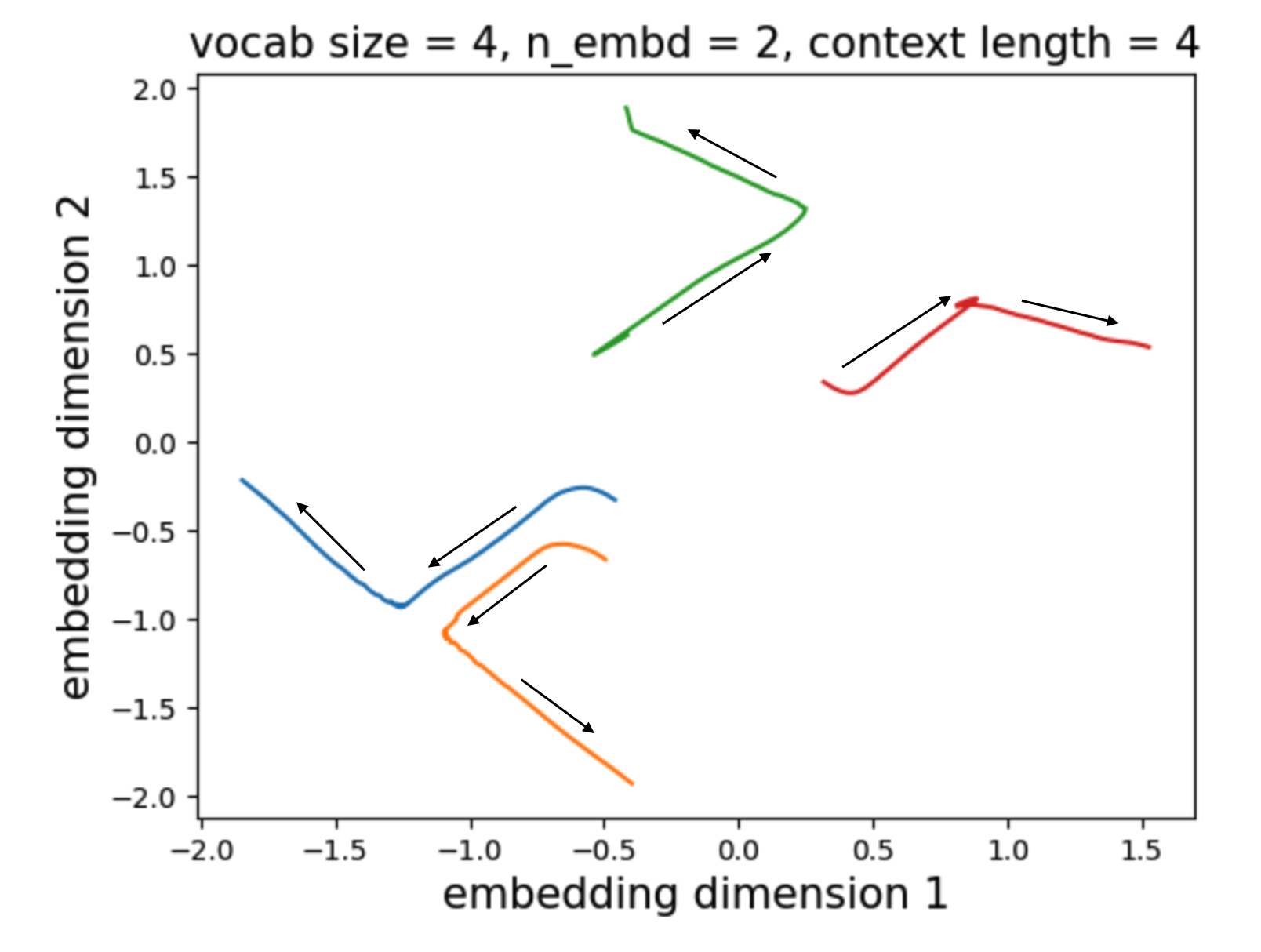
Explanation
We visualize the evolution of the embeddings (vocab size = 4) and find that there are two stages. In the first stage, the blue and yellow directions coincide, and the green and red directions coincide. As a result, the model cannot distinguish blue from yellow, or green from red, but it can distinguish which group a token belongs to. In the second stage, the elements within each group are finally separated.

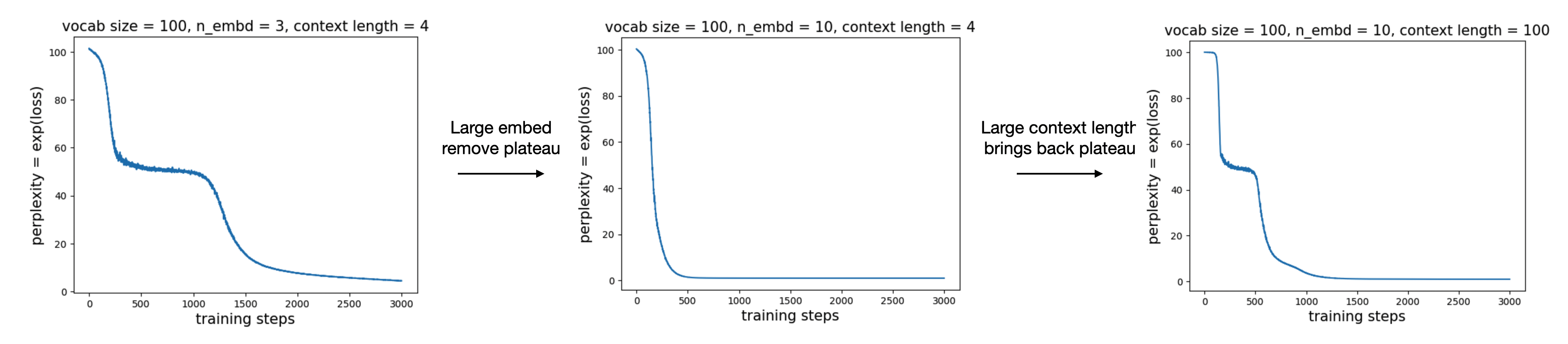
How general is the sticky plateau?

Although the sticky plateau phenomenon is interesting, how general is it? When the embedding dimension increases, there is enough resolution to distinguish different tokens, and the plateau may disappear. We indeed observe that this is the case. However, if we increase the context length, the sticky plateau comes back again. The picture, therefore, is that packing as many items as the context length into an embedding space of a given dimension leads to a situation where the presence or absence of a sticky plateau seems to correspond to a percolation phase transition.

Rank collapse

From the embedding visualizations above, we find that the embeddings initially expand along a single direction, and only later expand along another direction. Therefore, we expect that the effective dimensionality of the embeddings (defined in the same way as in the previous blog post), as well as the effective rank of the Q/K/V matrices, should exhibit corresponding dynamics.

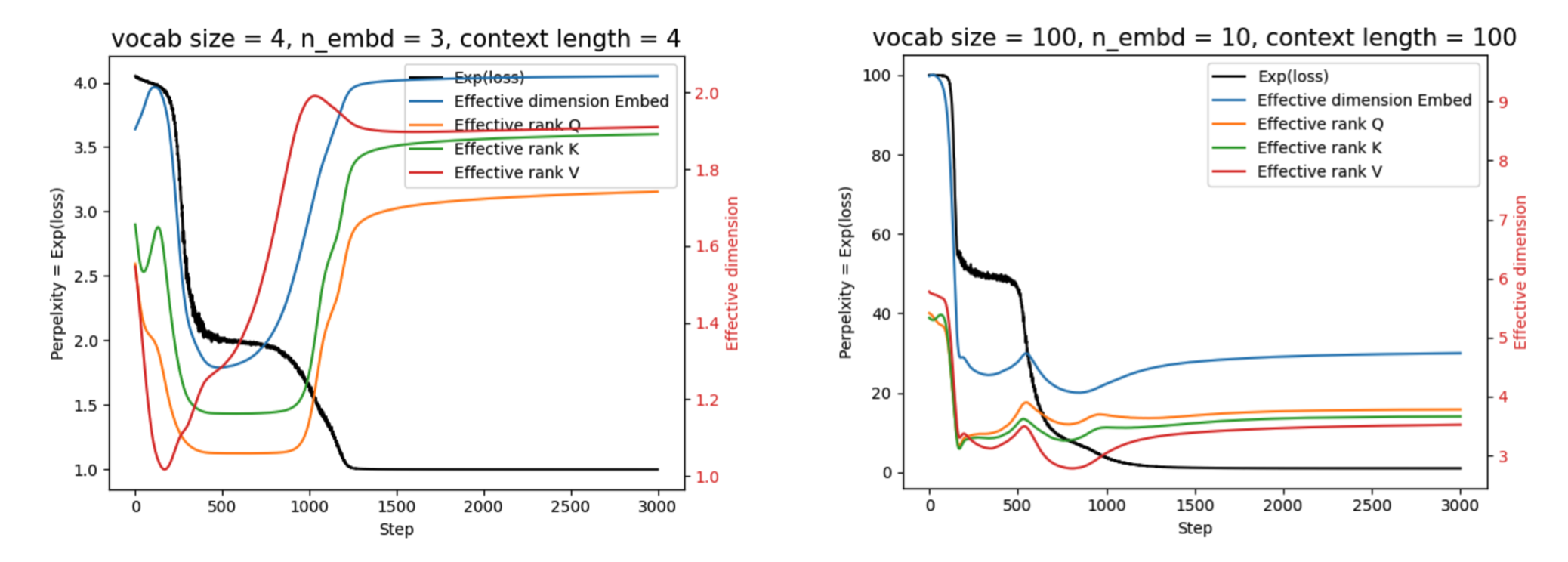
Left: Q/K also appear very sticky during the loss plateau, which may indicate that the dynamics of Q/K are the primary cause of the loss plateau.

Right: when all parameters are scaled up, Q/K become less sticky. Another observation that differs from the low-dimensional case is that when the loss decreases, the rank also decreases; when the loss plateaus, the rank increases; and when the loss decreases again, the rank decreases accordingly. The picture is that when the model is very clear about which features are useful, it aggressively exploits (grows) those features while (relatively) suppressing others, leading to a decrease in rank. When the loss reaches a plateau, the model explores which new features should grow, leading to an increase in rank. Once a useful new feature emerges, the model again exploits it, causing the rank to decrease.

Test on large models

The sticky plateau phenomenon predicts a loss plateau at \({\rm Log}(V/2)\), about 0.3 nats below \({\rm Log}(V)\). To the best of my knowledge, this plateau has never been observed in LLMs, maybe due to

• learning rate warmup has already nicely handled this problem
• we did not zoom in enough to see the plateau
• the sticky plateau is simply less relevant for large models

Either way, no matter if the sticky plateua is relevant for LLMs, we shoud better understand/control representation/rank collapses and the percolation phase transition.

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026sparse-attention-1,
  title={Sparse attention 1 -- sticky plateau and rank collapse},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/sparse-attention-1/}
}