Optimization 3 / Depth 2 -- Adding Bias After ReLU

Author: Ziming Liu (刘子鸣)

Motivation

I have been playing with the toy model of residual networks defined in depth-1. There is no specific goal—just exploratory poking around.

Representation collapse

Although the input \(x\) to the deep network is drawn from an isotropic Gaussian distribution, I observe that the output \(y\) appears to have a clearly non-zero mean across the batch dimension.

The histogram confirms this observation: while the mean of \(x\) is close to 0, the mean of \(y\) clearly deviates from 0.

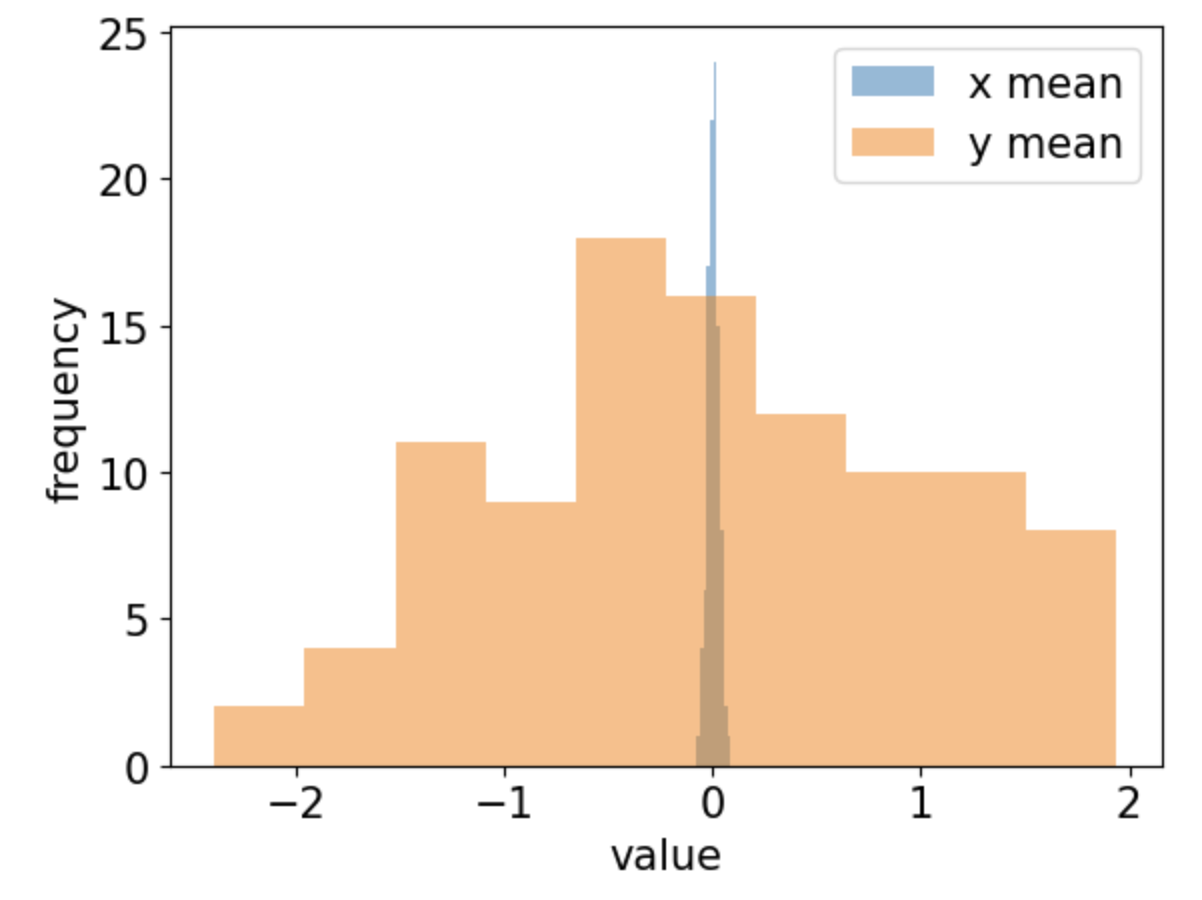
To quantify this deviation, we define \(\Delta\) as the standard deviation (across width) of the mean (across data points) of the output \(y\) at initialization.

We make two comments regarding the fact that \(\Delta > 0\):

• Origin: We hypothesize that this effect arises from ReLU inducing distribution shifts (see activation anisotropy).
• Judgment: This behavior is undesirable, and we would like to eliminate it (i.e., make \(\Delta \sim 0\)).

This raises the question: how can we eliminate it, and is it truly a feature or a bug?

Trick: adding bias after ReLU

Since the issue originates from ReLU shifting distributions toward the positive side, we can counteract this effect by adding a negative bias \(b\) after ReLU. Equivalently, the activation function becomes \({\rm ReLU}(\cdot) - b\).

We use a teacher–student setup. The teacher network is 10 layers deep, with input dimension 50 and hidden dimension 200. It uses post-norm and sets \(b = 0\). The student network shares the same architecture, but we sweep over different values of \(b\). Student networks are trained using the Adam optimizer with learning rate \(10^{-3}\) for 1000 steps. The results are shown below:

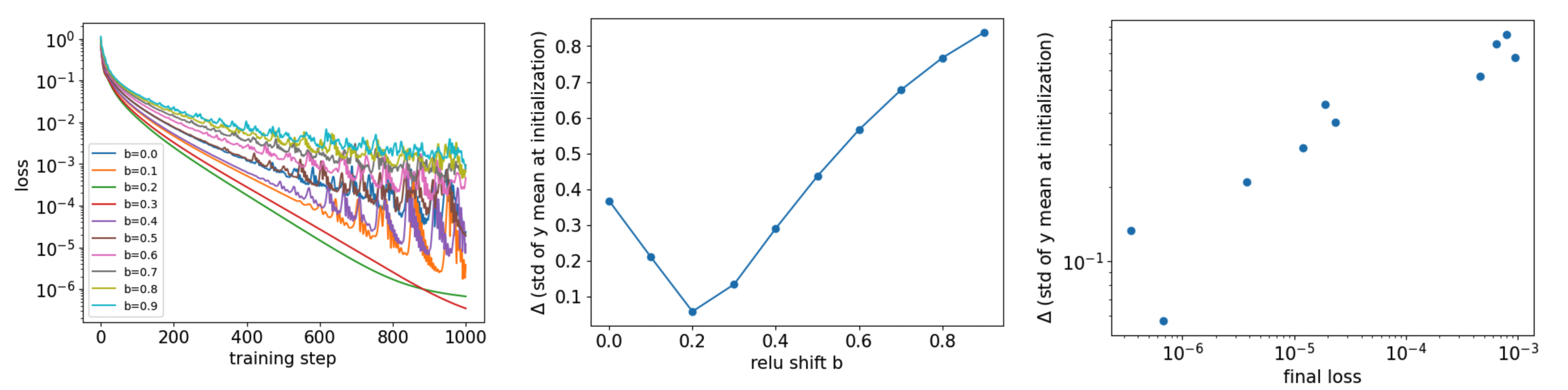
In the middle plot, we see that \(\Delta\) exhibits a U-shaped dependence on \(b\). Values \(b = 0.2, 0.3\) yield low \(\Delta\), which correspond to fast and smooth learning curves in the left plot. In the right plot, we explicitly show how the final loss correlates with \(\Delta\), revealing a clear positive correlation.

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026sparse-optimization-3,
  title={Optimization 3 / Depth 2 -- Adding Bias After ReLU},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/optimization-3/}
}