Optimization 1 -- Norm reparametrization

Author: Ziming Liu (刘子鸣)

Motivation

Recently, a number of architectures and optimizers have emphasized the role of normalization and/or learnable scales. To name a few:

2026-01-21: Hyperball optimization (link)
2026-01-13: Controlled LLM training on a spectral hypersphere (Link)
2026-01-08: Learnable Multipliers (Link)

Slightly less recent (last year :-) ), there are also the Muon optimizer and NVIDIA’s nGPT. These examples give a sense of how popular this direction has become.

On the one hand, the intuition is clear: when the step size is fixed, constraining parameters to lie on a small (but not too small) sphere allows the optimizer to make reasonable angular updates. On the other hand, we typically do not know the optimal scale in advance, and in some cases the optimal scale may be very large—or may even be infinite (e.g., logistic regression on linearly separable data). As a result, we would like an optimizer that can make both effective angular updates and effective radial (scale) updates.

To gain insight, we start with a toy example below.

Problem setup

Assume the optimal (flattened) weight of a model is \(W^*\in\mathbb{R}^N\). The initial weight is \(W_0\in\mathbb{R}^N\), and the loss is the MSE loss between \(W\) and \(W^*\), i.e., \(L = \|W - W^*\|_2^2 .\) An Adam optimizer with learning rate \(\eta\) is used to minimize the MSE loss.

When the target \(W^*\) is very far away, such that \(R \equiv \|W^*\| \gg \|W_0\| ,\) the time to reach the target is roughly \(t = \frac{R}{\sqrt{N}\eta} ,\) assuming (1) Adam behaves like SignGD with step size \(\eta\) so that each update has norm \(\sqrt{N}\eta\), and (2) updates from different steps are approximately parallel. In summary, the time complexity is \(O(R)\), which is not very good when \(R\) is large.

Can we do better?
Yes, we can!

By introducing a learnable norm scalar, the time can be reduced to \(O(\sqrt{R})\).
By further using a re-parametrization trick, the time can be reduced to \(O(\log R)\).

Step 1: Introducing learnable multipliers

To control both the angular direction and the norm, it is natural to introduce a learnable multiplier \(s\). The actual weight \(W\) is parameterized as \(W = s \hat{W},\) where \(\hat{W}\) may or may not be normalized.

When \(\hat{W}\) is learnable and not normalized, it is likely that \(|s| \to O(\sqrt{R}), \quad \|\hat{W}\| \to O(\sqrt{R}),\) since their roles are symmetric in the multiplication. Hence, the convergence time becomes \(t = O(\sqrt{R}/\eta).\) This is already better than \(O(R)\), but can we do even better?

Step 2: Re-parametrization

At each step, we compute the norm \(a \equiv \|\hat{W}\|_2\) and apply the following re-parametrization: \(\hat{W} \to \hat{W}/a, \quad s \to a s .\) This places \(\hat{W}\) on the unit hypersphere, representing the angular direction, while \(s\) captures the norm. Their product remains invariant under this re-parametrization. Training proceeds by interleaving gradient updates and re-parametrization steps.

In each update, the norm of \(\hat{W}\) changes from 1 (due to re-parametrization in the previous step) to \(1 \pm A\eta\), where \(A = A(N)\) depends on \(N\) and the gradient directions, which we do not worry about here. The key point is that this is a multiplicative (rather than additive) change. Therefore, growing the norm from 1 to \(R\) only takes \(O(\log R)\) steps.

Experiment

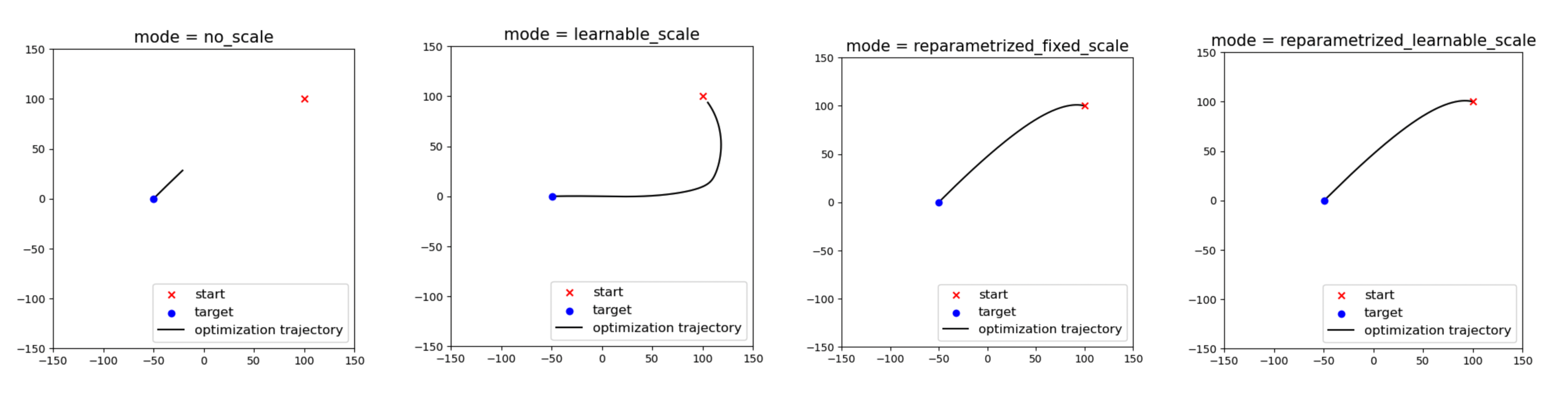
We conduct a 2D toy experiment. We set \(W_0 = (-50, 0), \quad W^* = (100, 100).\) We use Adam with learning rate \(\eta = 0.01\) and train for 3000 steps. We compare four modes:

no_scale: standard optimization (fixed multiplier \(s = 1\))
learnable_scale: learnable \(s\)
reparametrized_learnable_scale: re-parametrization, fix \(s = 1\) during the update step
reparametrized_fixed_scale: re-parametrization, allow \(s\) to update during the update step

Optimization trajectory:

Loss:

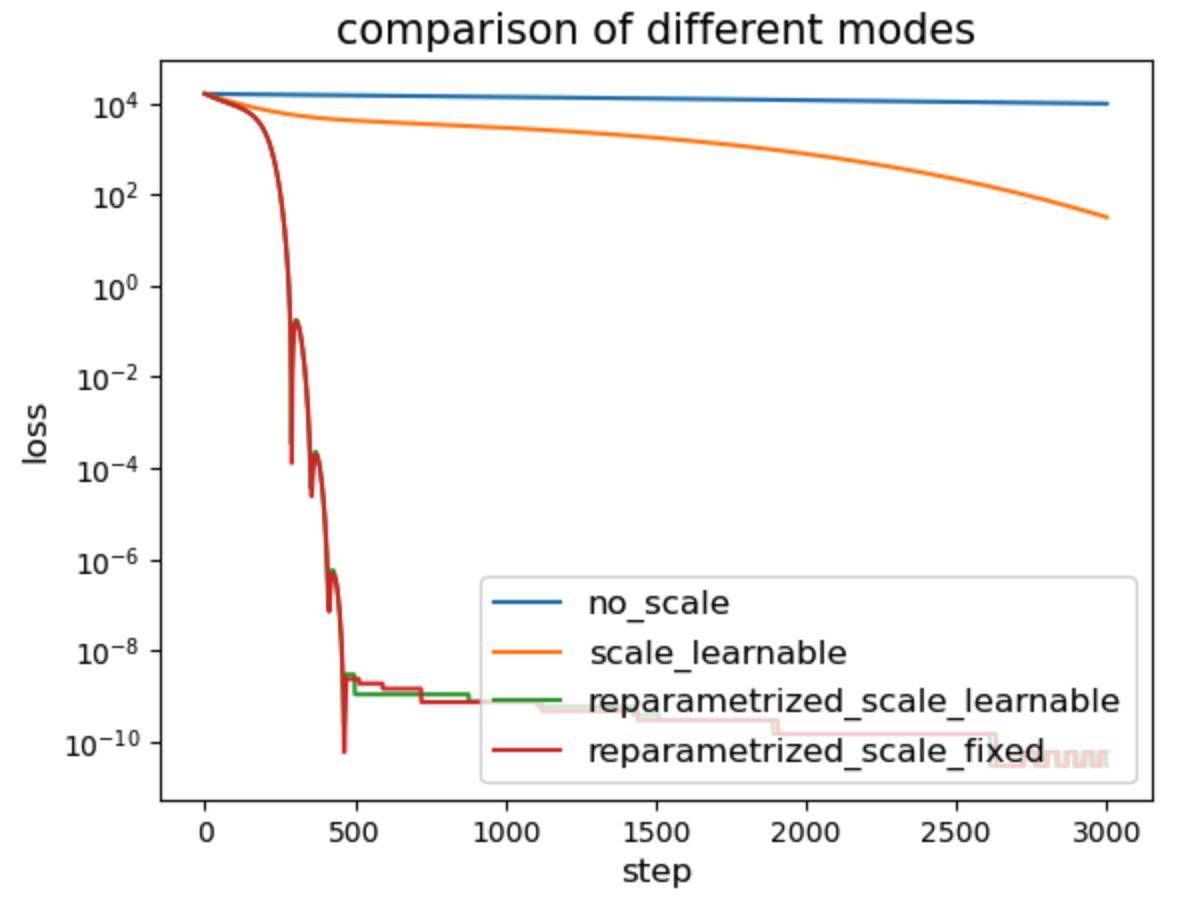
Observations:

As expected, re-parametrization > learnable scale > no scale.
With re-parametrization, whether the scale \(s\) is learnable or fixed during the update step does not seem to make a noticeable difference.

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026sparse-optimization-1,
  title={Optimization 1 -- Norm reparametrization},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/optimization-1/}
}