Multi-Head Cross Entropy Loss

Author: Ziming Liu (刘子鸣)

Motivation

In LLMs, next-token prediction is performed by passing the final-layer hidden representation through the LM head to produce logits, thereby projecting into the token space. The definition of cross-entropy implies that only the correct token receives a low loss, while any other token incurs a high loss. For example, if the correct token is “red,” predicting either “green” or “rabbit” results in a large loss. However, it is clear that green is much closer to red than rabbit is, since both are adjectives and both denote colors.

This motivates the following question: when designing the loss, should we take similarity between tokens into account? If token A and token B are similar in some respects, then if the model mistakenly predicts token B instead of token A, should it really be penalized as heavily as predicting a completely unrelated token C?

This idea is still quite abstract, and there are likely many concrete ways to implement it. In this post, we explore one possibility: multi-head cross-entropy loss. Inspired by multi-head attention—where different heads attend to different semantic aspects—multi-head cross-entropy aims to capture token similarity from multiple semantic perspectives.

Definition

Standard Cross-Entropy

Let the input representation to the LM head be $x \in \mathbb{R}^D$ and the LM head weights be $W \in \mathbb{R}^{V \times D}.$ The LM head output (i.e., the logits) is $y = W x \in \mathbb{R}^V,$ where $V$ is the vocabulary size. Standard cross-entropy computes the loss between $$y$ and the ground-truth label.

Multi-Head Cross-Entropy

We split $x$ into $H$ heads: $x = [x_1; x_2; \cdots; x_H], x_i \in \mathbb{R}^{D/H}$. Similarly, we split $W$ into $H$ parts: $W_i \equiv W[:,i\frac{D}{H}:(i+1)\frac{D}{H}] \in \mathbb{R}^{V\times D/H}.$ The logits for the $i$-th head are $y_i = W_i x_i \in \mathbb{R}^V.$ After applying Softmax, we define a probability distribution $p_{i,j} = \frac{\exp(y_{i,j})}{\sum_{j=1}^{V} \exp(y_{i,j})},$ which represents the probability of token $j$ under the $i$-th semantic head.

How should we aggregate different heads? Here we simply sum the probabilities (without a rigorous justification, and many other choices are possible): $p_j = \sum_{i=1}^{H} p_{i,j}.$ The corresponding aggregated logit is $y_j = \log(p_j).$

Example: Toy Language

Dataset

We assume each token has two features:

Part of speech: noun or verb
Topic: mathematics or sports

Grammar: nouns and verbs alternate: $\text{noun} \rightarrow \text{verb} \rightarrow \text{noun} \rightarrow \text{verb} \rightarrow \cdots$

Topic: within a sentence, the topic is consistent—either mathematics or sports.

Thus, we have four classes of tokens:

A: math nouns
B: math verbs
C: sports nouns
D: sports verbs

Each class contains 10 tokens (randomly chosen). Valid sentences look like:

\[[A8] \rightarrow [B2] \rightarrow [A5] \rightarrow [B6] \rightarrow [A1] \rightarrow [B7] \rightarrow \cdots\] \[[C2] \rightarrow [D1] \rightarrow [C6] \rightarrow [D2] \rightarrow [C10] \rightarrow [D3] \rightarrow \cdots\]

Model

We consider a bi-gram model, which predicts the next token based on the previous token. The model uses an MLP, with weight tying between the embedding layer and the LM head.

Results

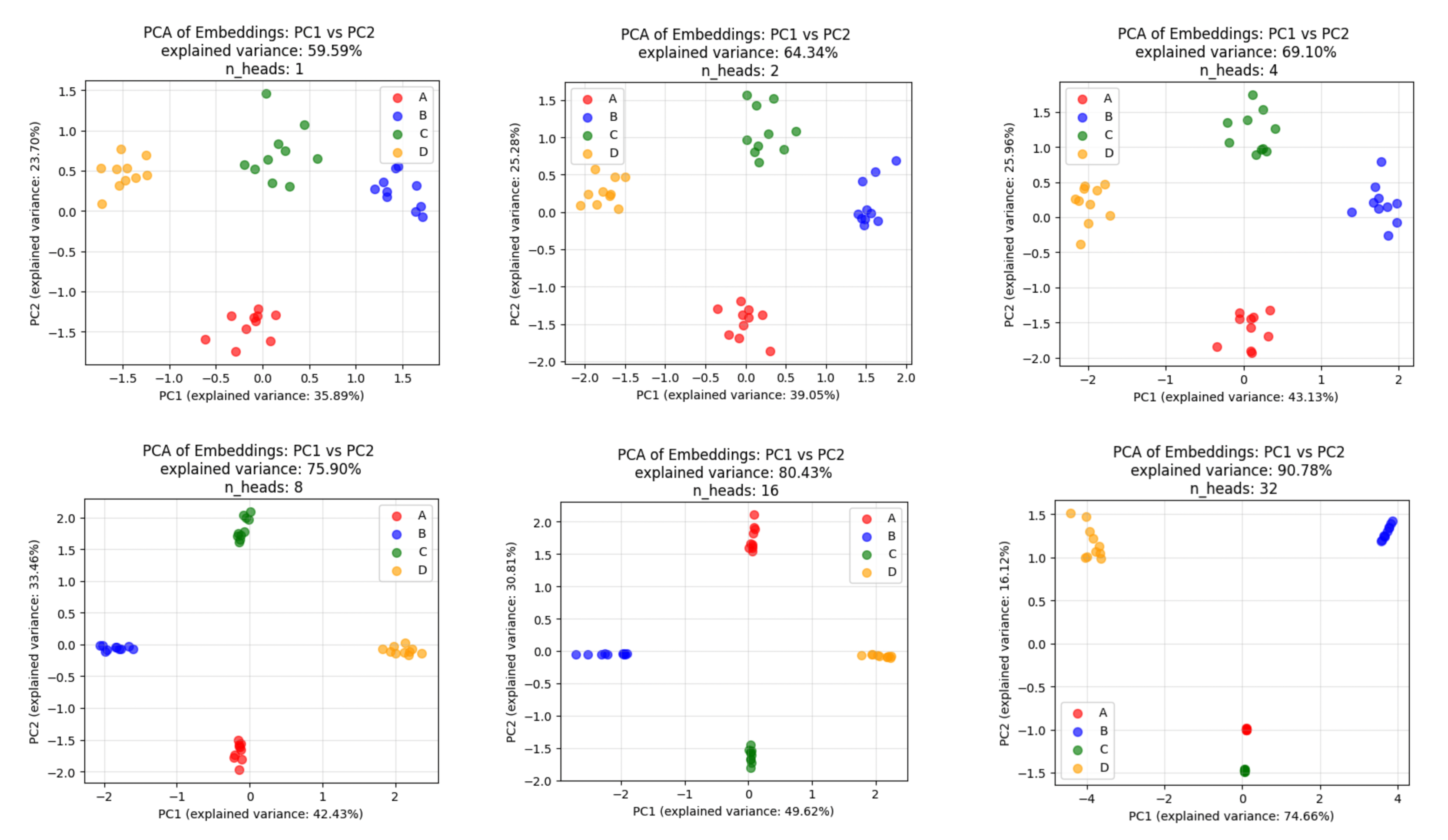
We perform PCA on the embedding space and project each token embedding onto PC1/PC2. We find that as the number of heads increases:

Clustering improves.
The explained variance increases (i.e., the representation becomes more low-dimensional).

Grokking

I also randomly tried a grokking (modular addition) setup and found that multi-head cross-entropy does not significantly accelerate grokking. This was not particularly surprising—I did not have a strong prior for why it should help. This result is reasonable because, in modular addition, tokens essentially have only a single semantic dimension (numerical value), so there is no meaningful notion of multiple semantics for different heads to exploit.

Questions

Can we design a more suitable toy dataset that enables more mechanistic interpretability?
Does it make sense to apply multi-head cross-entropy loss to large language models?

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026multi-head-cross-entropy,
  title={Multi-Head Cross Entropy Loss},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/multi-head-cross-entropy/}
}