MLP 2 -- Effective linearity, Generalized SiLU

Author: Ziming Liu (刘子鸣)

Motivation

MLPs are powerful because they include nonlinear activation functions. But how effectively do they actually use this nonlinearity? If we perform a linear regression between the MLP inputs and outputs and obtain \(R^2 \approx 1\), then the MLP is not making effective use of its nonlinearity.

Problem setup

We use the same setup as in depth-1. Both the teacher and the student networks are residual networks with MLPs. The teacher network uses the SiLU activation function, while we vary the activation function of the student network. We measure the \(R^2\) values for the MLPs in all layers and track how these quantities evolve during training.

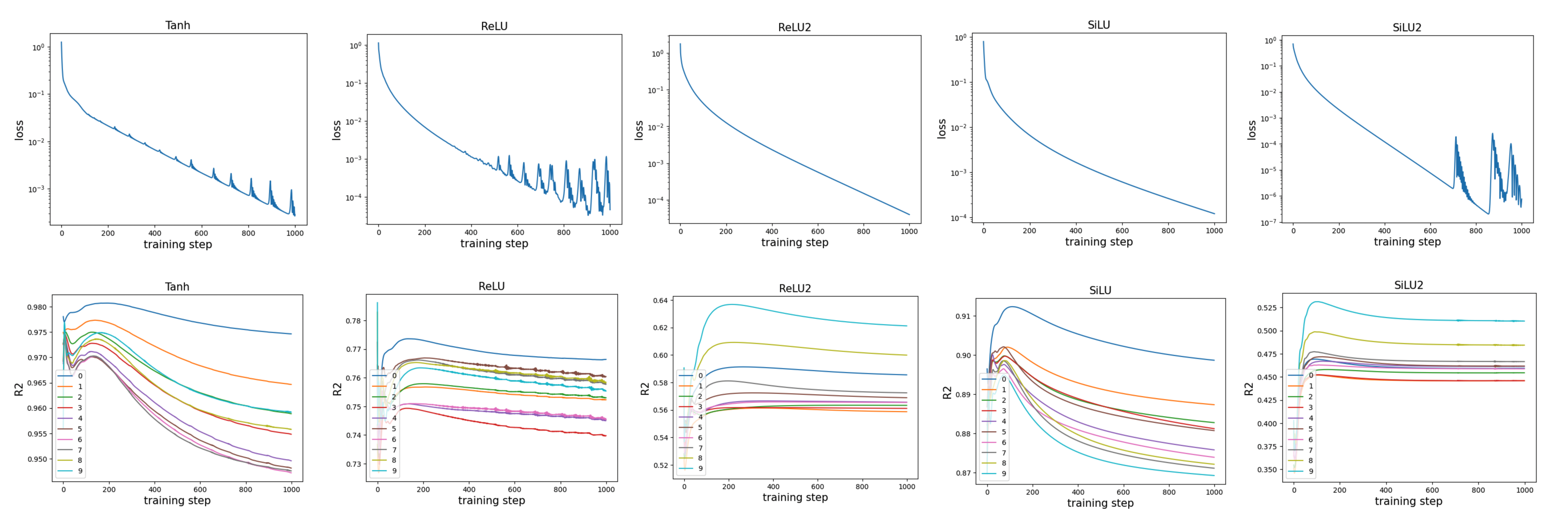
We observe that lower \(R^2\) values tend to correspond to lower losses, which aligns with the intuition that a lower \(R^2\) indicates stronger nonlinearity. One could attempt to minimize \(R^2\) further—for example, by using high-frequency sine functions—but this would likely harm trainability. There appears to be a trade-off between stability and nonlinearity.

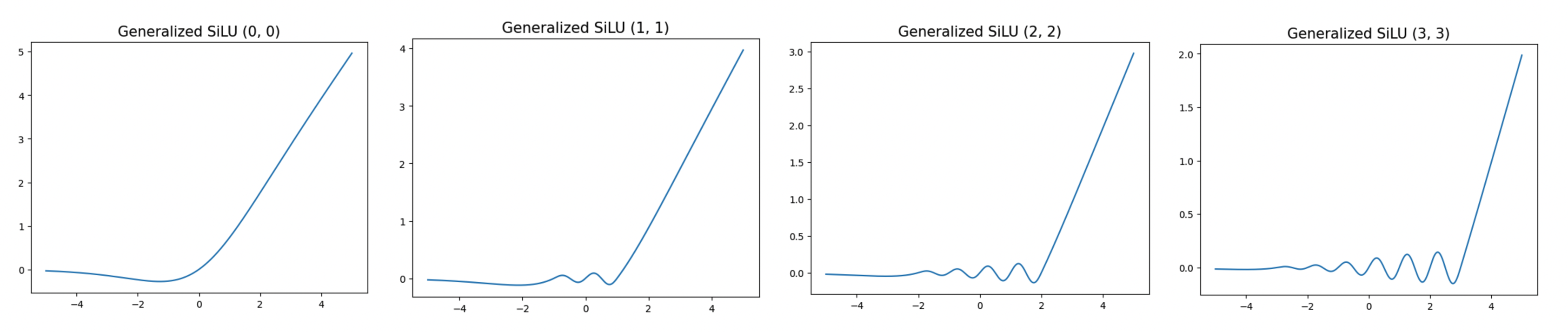
Generalized SiLU

Can we define a family of activation functions for which SiLU is a special case, while also allowing for more oscillatory behavior? We define a generalized SiLU function as follows:

The definition in Python code is shown below:

SiLU corresponds to generalized SiLU with parameters (0, 0). We find that generalized SiLU with parameters (0, 1) or (1, 1) can achieve extremely low loss.

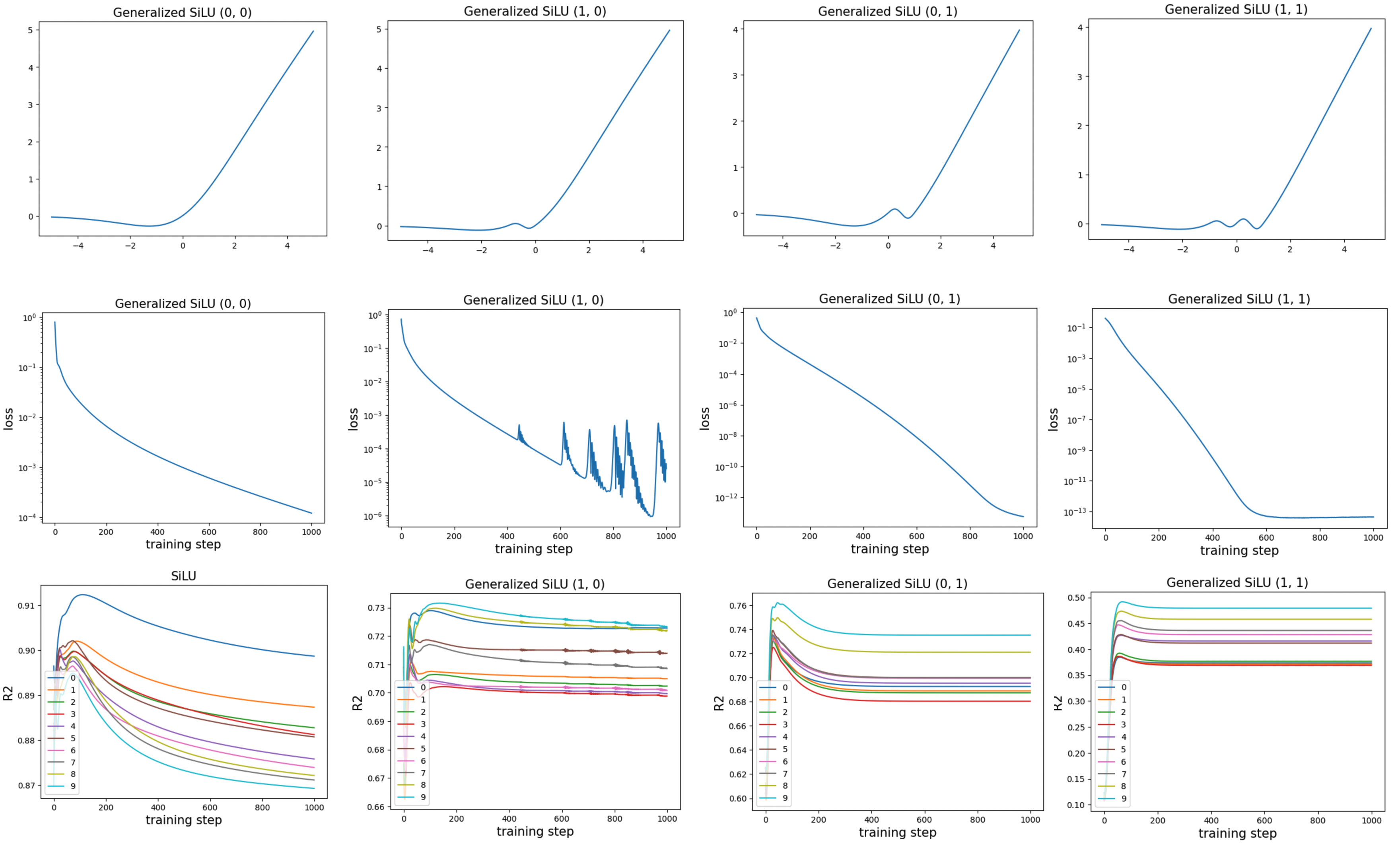
Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026mlp-2,
  title={MLP 2 -- Effective linearity, Generalized SiLU},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/mlp-2/}
}