MLP 1 -- Gating is good for polynomials

Author: Ziming Liu (刘子鸣)

Motivation

Gated MLPs are widely used in modern language models. Given an input \(x\), the hidden representation of a gated MLP is \(\sigma(W_g x) \odot W_v x .\) It is often argued that gating promotes sparsity, multiplicative structure, conditional computation, and more stable training. This is far too large a topic to be fully explored in a single blog post. In this article, we narrow the scope to polynomial fitting. If learning a Taylor expansion is important for neural networks, then learning polynomials is a necessary prerequisite.

Polynomials

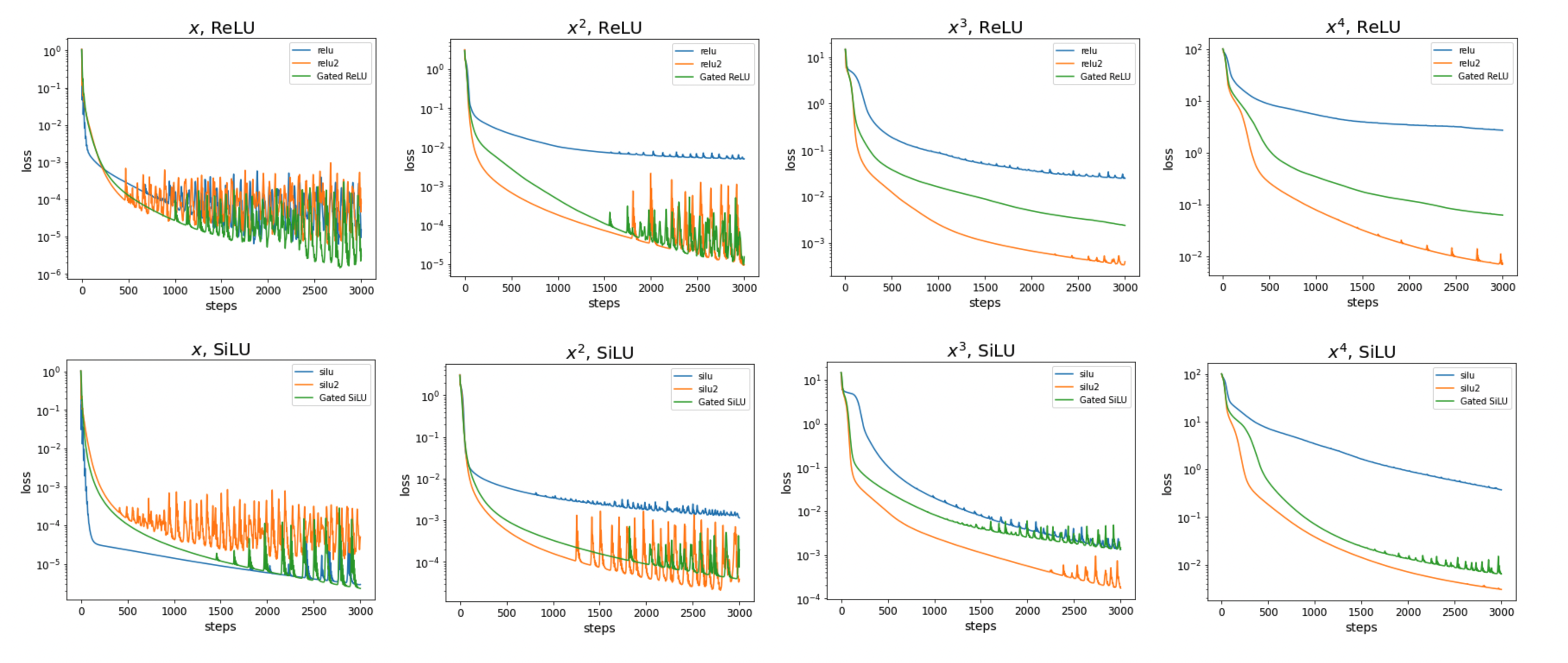
For both ReLU and SiLU activations, gated MLPs (green) consistently outperform non-gated MLPs (blue) when fitting \(x^n\) for all \(n \ge 2\). We also compare against non-gated MLP but with the activation function squared (orange), and find that squared activation functions can achieve strong performance—sometimes even better than gated networks.

A rough equivalence

We observe that as \(\epsilon \to 0^+\), a Taylor expansion gives \(\sigma((w+\epsilon)x) - \sigma((w-\epsilon)x) \approx 2\epsilon x \sigma'(wx) .\) This suggests a rough “equivalence” between \(\sigma(x)\) and \(x \sigma'(x)\), where \(x \sigma'(x)\) can be interpreted as a gate. For gated ReLU networks, since \(\sigma'(x) = {\rm ReLU}\), this implies \(\sigma(x) = {\rm ReLU}^2\). In other words, a gated ReLU network is roughly equivalent to a non-gated ReLU2 network.

So far, this is not meant to be mathematically rigorous—just a hand-wavy but potentially useful intuition. Once we have a useful gate, it can be converted to a useful activation function for free (except for doing integration).

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026mlp-1,
  title={MLP 1 -- Gating is good for polynomials},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/mlp-1/}
}