Emergence of Induction Head Depends on Learning Rate Schedule

Author: Qingyu Qu (屈清宇), Ziming Liu (刘子鸣)

Motivation

Induction heads are crucial for in-context learning abilities. However, the dependence of its emergence on learning rate schedule is fewly discussed. Indeed, at first glance, the emergence of induction heads should depend more, if not exclusively, on structure of data. But it makes sense to think of the learning rate schedule because such a delicate module like induction head should not use a large learning rate to construct. Below we make an early exploration of the dependence of induction head emergence on learning rate schedule.

Problem setup

We adopt a similar setup as Olsson et al., where a two layer transformer(with mlps) is trained on openwebtext data. The details are as follows.

Model
The model here is a two layer transformer(with mlps). Embedding dimension is 768, number of heads per layer is 12, these numbers are chosen to be the same as Olsson et al.. Weight tying between embedding and unembedding is used. The implementation of the model is a modified version of NanoGPT. The train loop is also basically train.py in NanoGPT.

Dataset
We use openwebtext as the training dataset, because we found that natural language data is important for induction head emergence. We also found many papers arguing that induction heads emerge from synthetic data, but our “induction heads” emerging from synthetic data can rarely perform well on repeated random sequences, which we think is an important ability of induction heads shown in Olsson et al..

Induction score To measure the emergence of induction heads, we adopt a similar strategy as Olsson et al., which they called prefix matching score. We test the model checkpoint on a repeated random sequence, and calculate a head’s attention weight given to the token we expect an induction head to attend to – the token where the prefix matches the present context. We adopt the largest induction score among all heads to be the induction score of the model. In other words, a large induction score means that there is at least one head showing induction attention pattern on repeated random sequences.

Fixed learning rate fails to give rise to induction heads.

We train the same model using the same data. The only difference is that the learning rate is among \(\{6\times 10^{-5}, 6\times 10^{-4}, 6\times 10^{-3}\}\). We train the model until the accumulated learning rate reaches threshold 3, i.e. we train the model for \(\{5\times 10^4, 5\times 10^3, 5\times 10^2\}\) steps. The goal of this trick is to balance the time effect introduced by learning rate, i.e. 1 step under 0.1 learning rate is roughly 100 steps under 0.01 learning rate.

As shown by the figure, the induction score is low. In fact, in our setup, a random sequence of length 10 is repeated 5 times, so the random guess induction score is around 0.1. One might argue we do not train enough, but below we show that we can get induction heads with these many steps(or accumulated learning rates) using learning rate warmup.

Learning rate warmup to the right plateau is important for induction heads emergence

In this section, we first warm up the learning rate for 100 steps to a plateau among \(\{6\times 10^{-5}, 6\times 10^{-4}, 6\times 10^{-3}\}\), then the learning rate will be stable until the end of training.

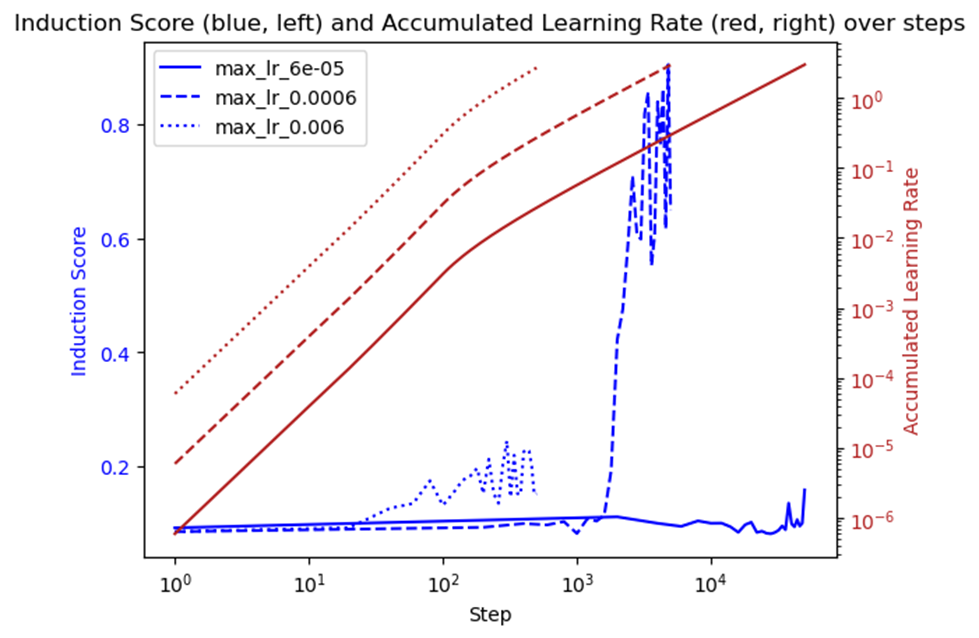
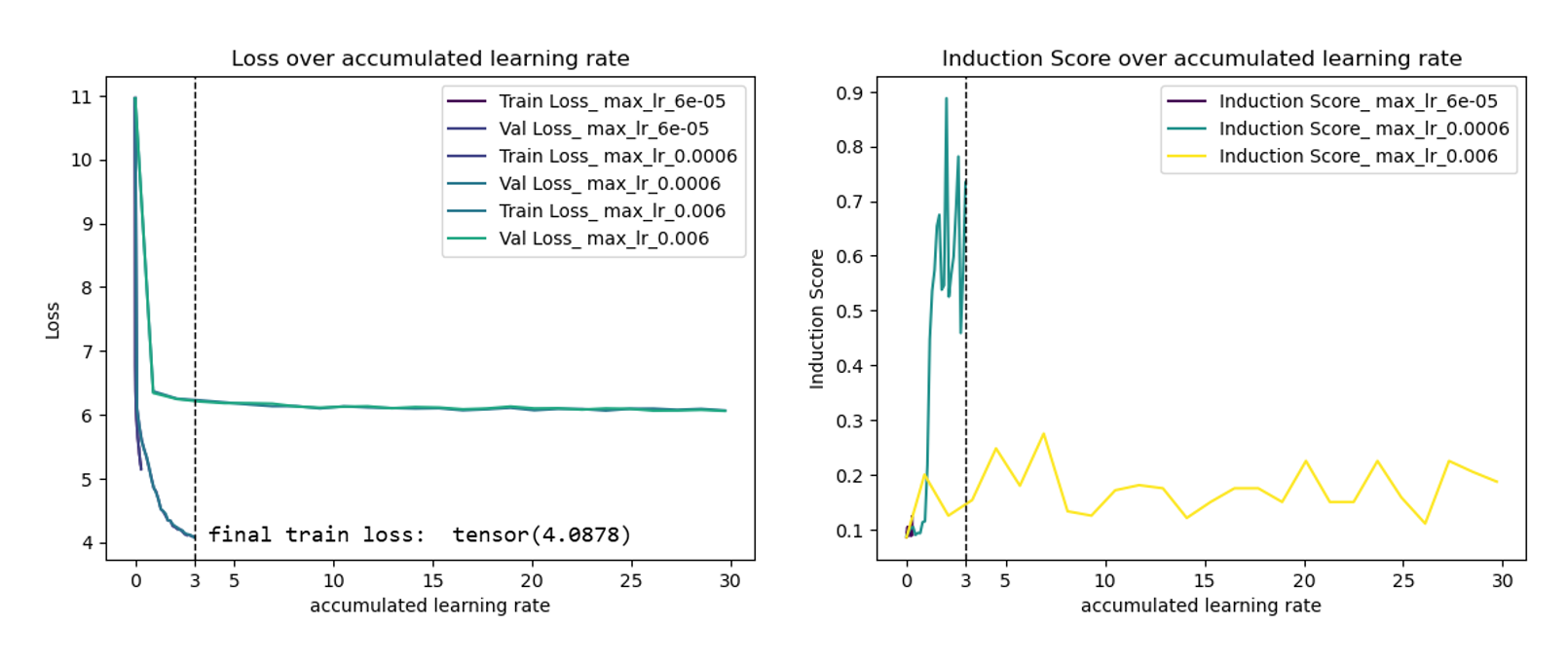
We observe that, in our experiment, the plateau learning rate can be neither too large nor too small. One may doubt that our training in \(6\times 10^{-3}\)case is not enough. The following figure shows that, even though we train 5000 steps in \(6\times 10^{-3}\)case, induction heads still miss.

Learning rate warmup iters affect the speed of emergence of induction heads

Since we found that \(6\times 10^{-4}\) is the right plateau for learning rate warmup, we test the learning rate schedule with different warmup iterations to this plateau. The result is as follows.

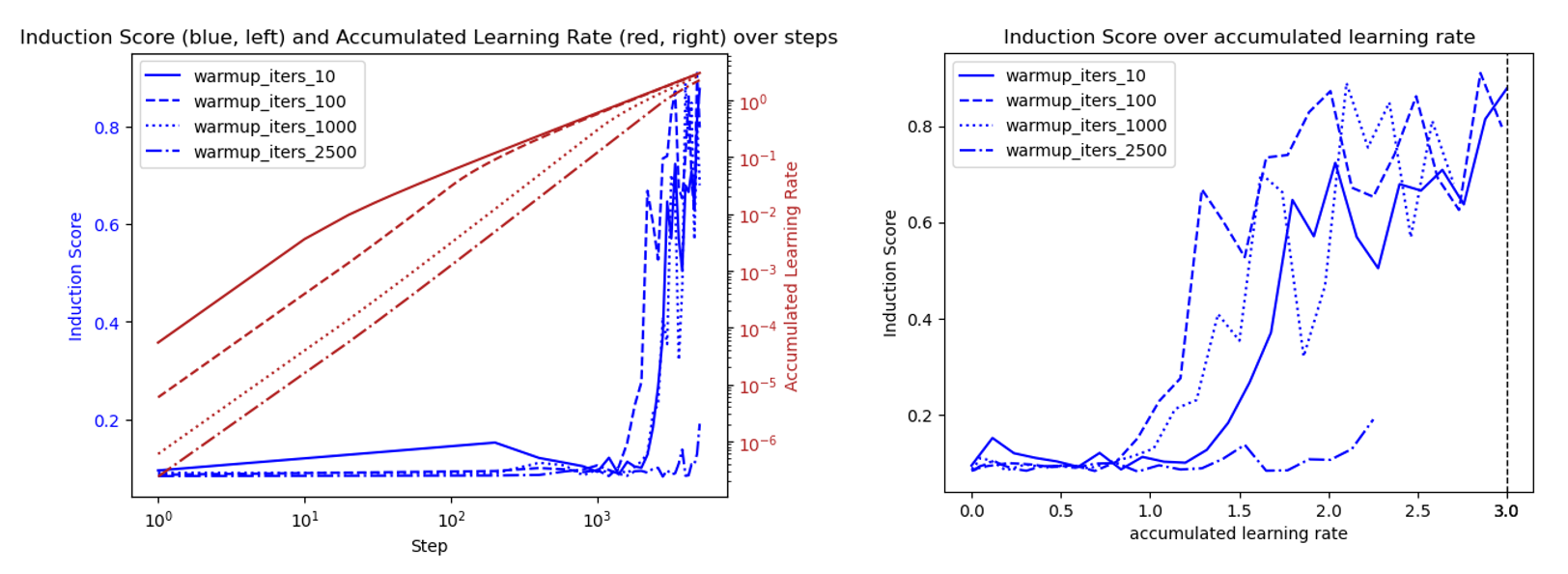
As shown by the figure above, warmup iter=100 leads to the fastest emergence of induction heads.

Learning rate decay has little effect on induction head emergence.

This may sound counter-intuitive since learning rate decay is crucial for constraining the model not to overfit the data, which will destroy the generalisation solution like induction head. However, for a small model trained on a big dataset like openwebtext, maybe overfitting can hardly happen, and this is also verified by the train and validation loss are always the same during the course of training. At the same time, learning rate decay has little effect on the final accumulated learning rate since most of the accumulated learning rate is contributed by the peak learning rate. Below, we train the model for 5000 steps and ignore the little difference in final accumulated learning rate.

We use a linear warmup of 100 steps and use cosine decay to a min_lr.

If the plateau learning rate = \(6\times 10^{-3}\), induction heads will not emerge.

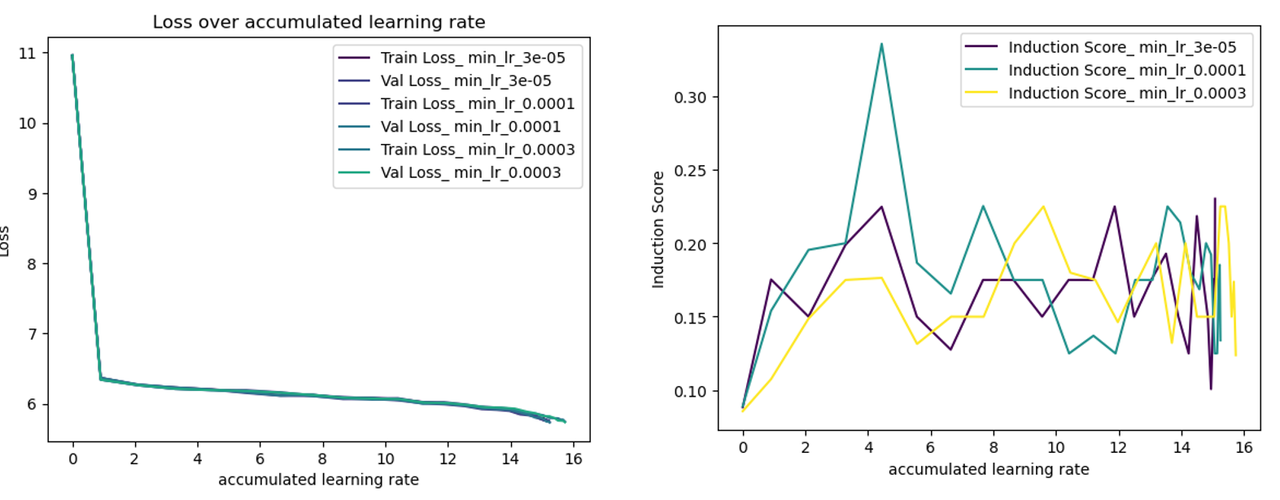
If the plateau learning rate = \(6\times 10^{-4}\), induction head will emerge.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{qu2026induction-head-lr-schedule,
  title={Emergence of Induction Head Depends on Learning Rate Schedule},
  author={Qu, Qingyu; Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/induction-head-lr-schedule/}
}