Diffusion 1 -- Sparse and Dense Neurons

Author: Ziming Liu (刘子鸣)

Motivation

I was reading this paper, “Unconditional CNN denoisers contain sparse semantic representation of images”, which reports an intriguing observation: some neurons (CNN channels) are sparsely activated, while others are densely activated. The authors interpret this as follows: sparse neurons correspond to specific semantic features (e.g., a dog), and therefore activate only when that feature is present in the input image; dense neurons, by contrast, capture more global properties such as lighting, and hence activate across almost all images.

The goal of this article is to propose a minimal toy setup in which such a division of labor naturally emerges.

Problem setup

Dataset
We consider a simple scenario in which a “dog” may or may not appear under various “lighting conditions.” We model the dog as a Gaussian packet and the lighting as a constant offset. An “image” (a 1D function) is therefore given by \(I(x) = L + A {\rm exp}(-\frac{-(x-x_c)^2}{2 w^2}),\) where \(L\sim U[0,0.5]\), \(A\sim {\rm Bern}(p)\) (with probability \(p=0.2\) of being 1 and probability \(1-p=0.8\) of being 0), \(x_c\sim U[-0.8,0.8]\), and \(w=0.05\). We sample 100 such “images.”

Model
We adopt a 1D U-Net architecture. The input dimension is 128. The network consists of 3 downsampling blocks (each producing 8 output channels) and 3 upsampling blocks. We deliberately choose a small number of channels (8), since the task is simple and our goal is to understand what each individual channel is doing. The U-Net is trained as a denoiser with noise level \(\sigma = 0.1\) (again for simplicity).

Output of the first downsampling block

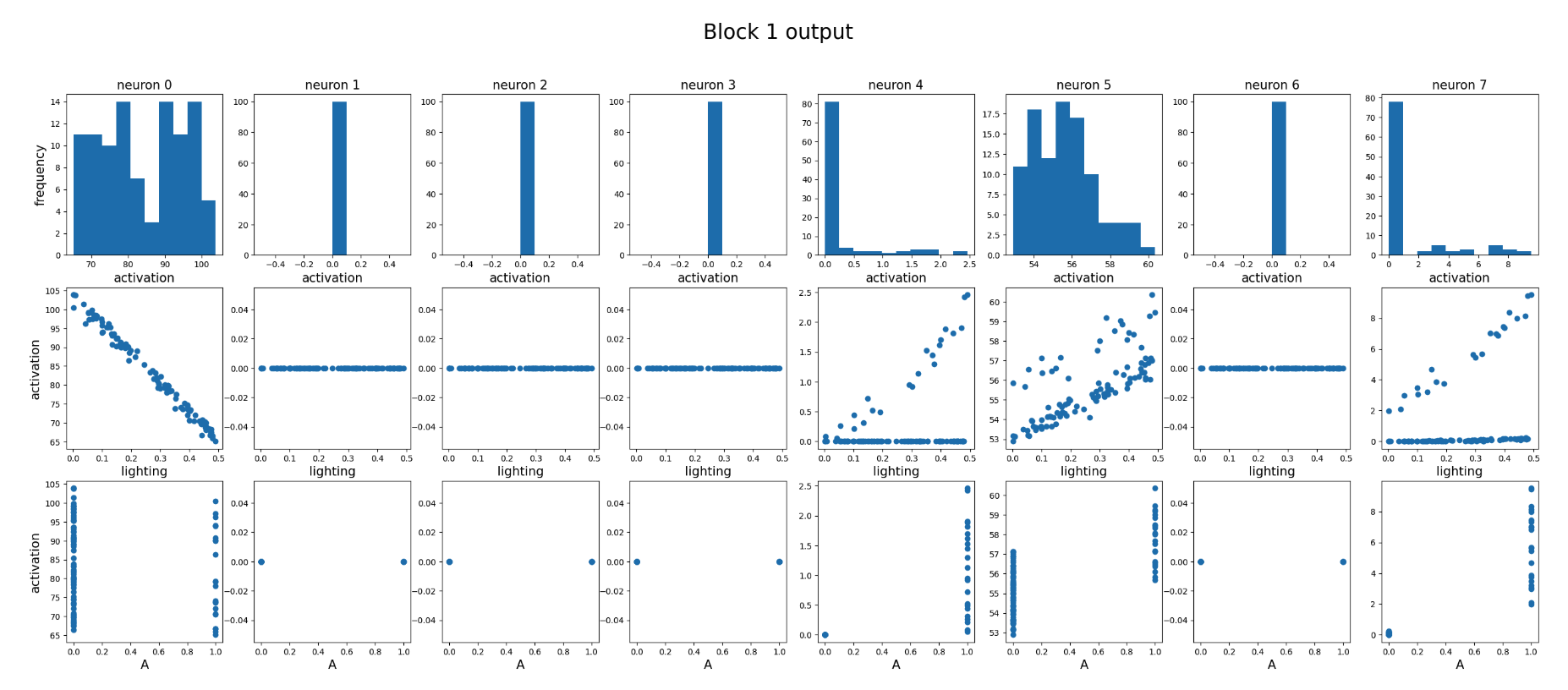
Each column corresponds to one neuron (channel), for a total of 8 channels.

• First row: activation distribution of each neuron over the dataset.
• Second row: activation versus lighting.
• Third row: activation versus \(A\) (1 when the Gaussian is present, 0 otherwise).

We find four distinct types of neurons:

• Dead neurons: neurons 1, 2, 3, and 6.
• Pure lighting neuron: neuron 0.
• Pure Gaussian-detection neurons: neurons 4 and 7.
• Mixed lighting + Gaussian detection neuron: neuron 5.

We also include results for blocks 2 and 3.

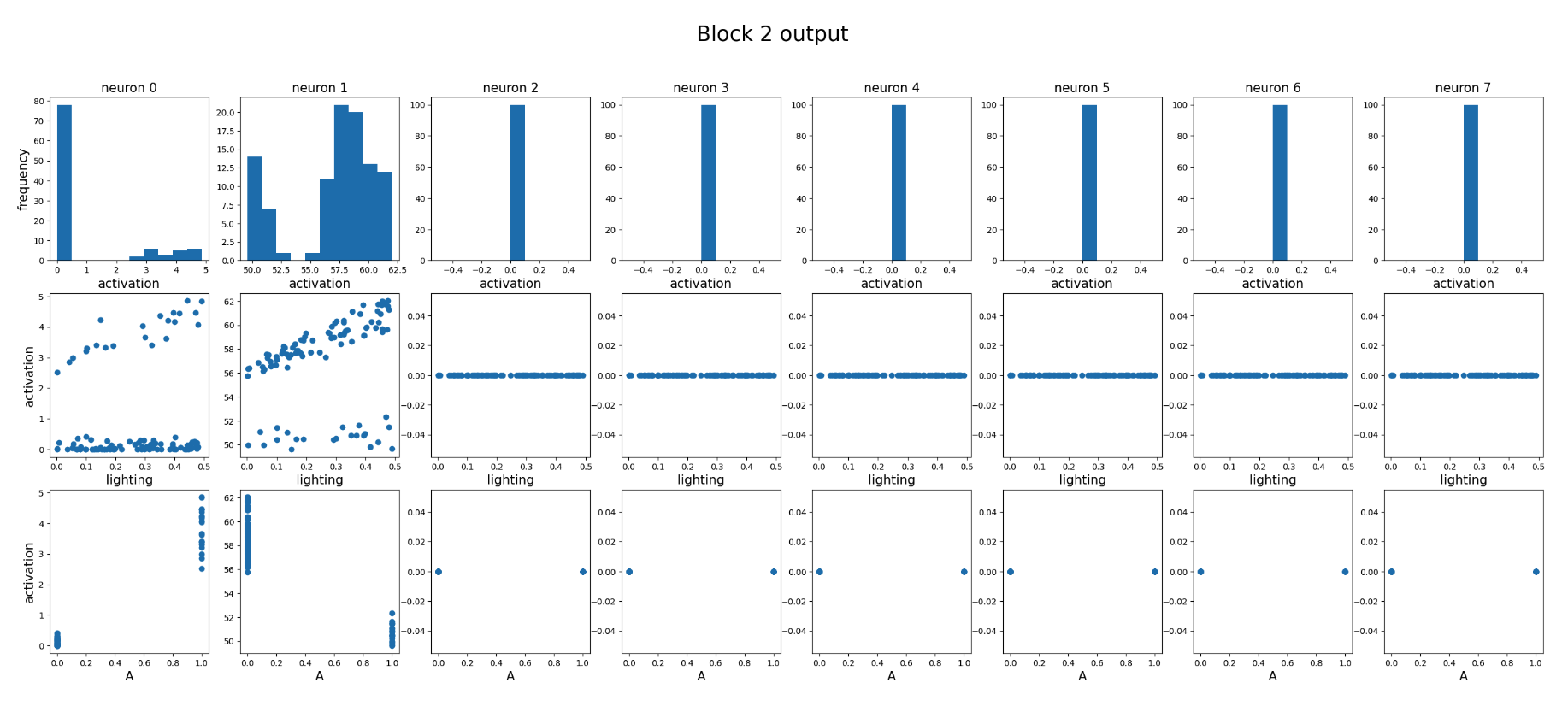
In block 2, neurons 2–7 are all dead. Neuron 0 is selective to the Gaussian, while neuron 1 exhibits mixed behavior.

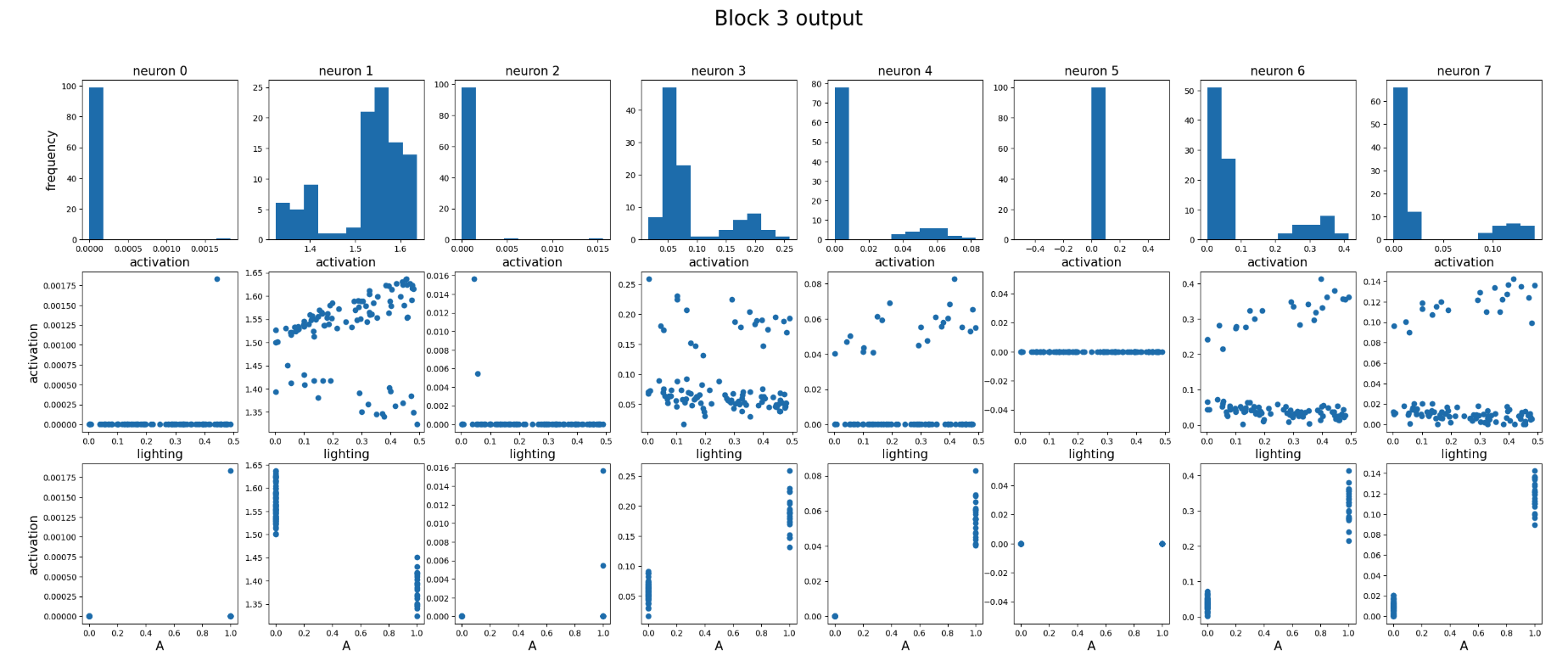
In block 3, neurons 0, 2, and 5 are dead. Neurons 1 and 3 show mixed behavior, while neurons 4, 6, and 7 are selective to the Gaussian.

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026diffusion-1,
  title={Diffusion 1 -- Sparse and Dense Neurons},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/diffusion-1/}
}