Bigram 1 -- Walk on a Circle

Author: Ziming Liu (刘子鸣)

Motivation

Markov chains are simple yet remarkably powerful structures. A natural question is therefore: can transformers learn Markov chains efficiently? For a first-order Markov chain, the next state depends only on the current state, which is equivalent to a bigram structure. This post is the first in a new Bigram series, where we will feed various bigram datasets to transformers and study their behavior.

In this article, we focus on one of the simplest nontrivial cases: a random walk on a circle.

Problem setup

Dataset

We consider a random walk on a 1D circular manifold, obtained via the following simplifications:

from a 2D Manhattan map to a 2D grid (ignoring, for example, diagonal streets),
from a 2D grid to a 1D grid,
imposing periodicity (the added symmetry may simplify analysis).

Suppose there are 10 points on the circle. Typical trajectories look like

\[[0] \rightarrow [1] \rightarrow [0] \rightarrow [9] \rightarrow [8] \rightarrow [7] \rightarrow [8] \rightarrow [7] \rightarrow \cdots\] \[[2] \rightarrow [1] \rightarrow [2] \rightarrow [3] \rightarrow [4] \rightarrow [5] \rightarrow [4] \rightarrow [3] \rightarrow \cdots\]

Model

Since the next token depends only on the current token, a context length of 1 is sufficient. This allows us to greatly simplify the model:

Context length = 1
No positional embedding (positional information is unnecessary when the context length is 1)

The dataset thus reduces to a pure bigram problem. The model consists of

a single attention layer (1L), no MLP,
embedding and unembedding layers with tied weights.

Because the context length is 1, only the OV matrix plays a role. Without the OV matrix, and with tied embedding/unembedding weights, each token can only map to itself, making the random-walk task impossible.

Our primary interest is in visualizing the evolution of the embedding vectors, as these can reveal whether a world model—namely, the circle—is being learned. If such a world model is learned, we would expect the tokens \(0, 1, 2, \cdots, 10\) to arrange themselves along a circle in embedding space.

We will vary the embedding dimension \(n_{\rm embd}\). In principle, an embedding dimension of 2 should suffice, since a circle can be naturally embedded in 2D Euclidean space.

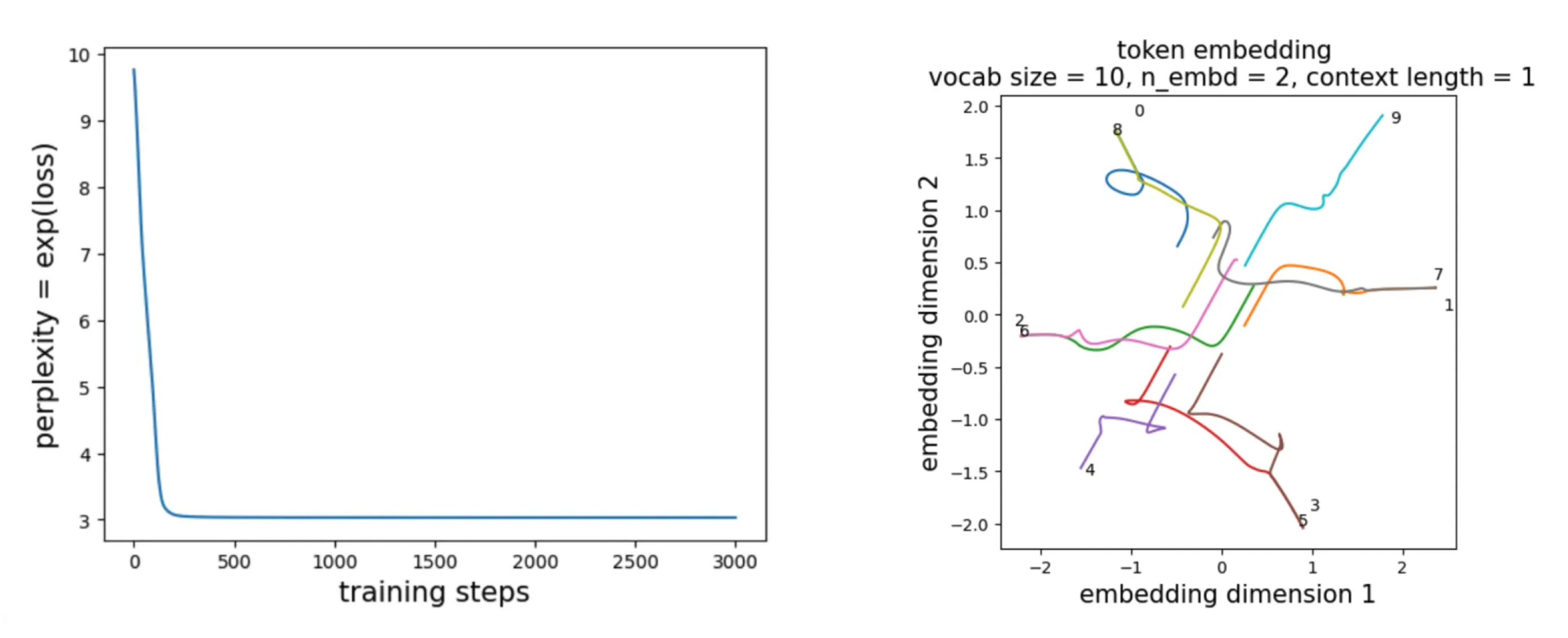
Observation 1: \(n_{\rm embd} = 2\) is not enough

We fix the vocabulary size to 10.

For \(n_{\rm embd} = 2\), the left plot below shows that the perplexity only decreases to about 3—corresponding to confusion among roughly three choices—whereas the optimal perplexity is 2. This indicates that \(n_{\rm embd} = 2\) is insufficient. The right plot shows that the embedding vectors do learn some notion of continuity (for example, 4 is close to 3 and 5, and 9 is close to 0 and 8), but the overall geometry is inconsistent (for instance, 1/7 lies diagonally relative to 2/6).

In contrast, \(n_{\rm embd} = 4\) is sufficient to reach the optimal perplexity of 2.

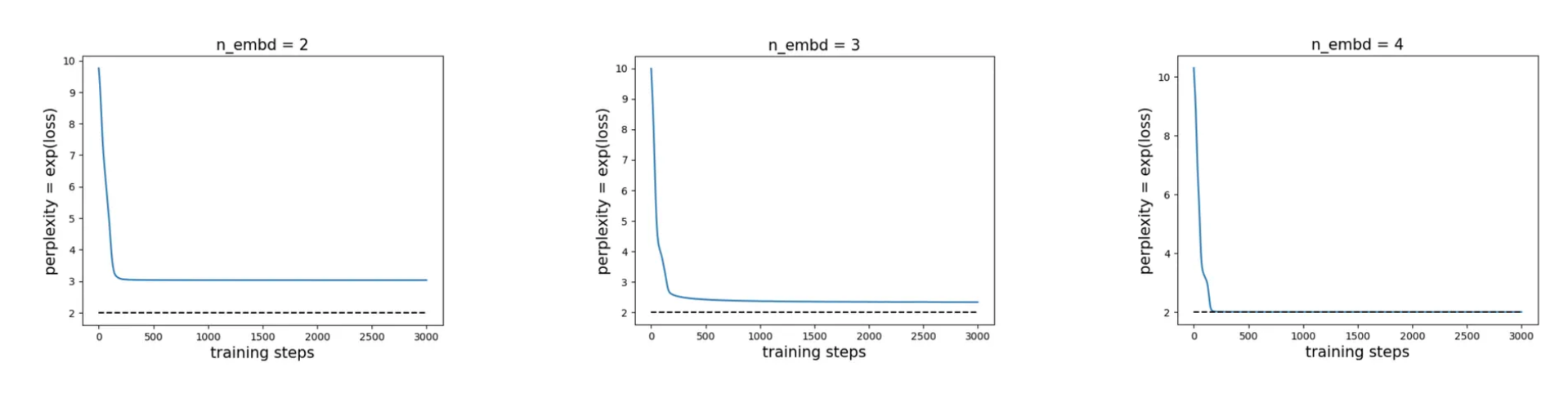
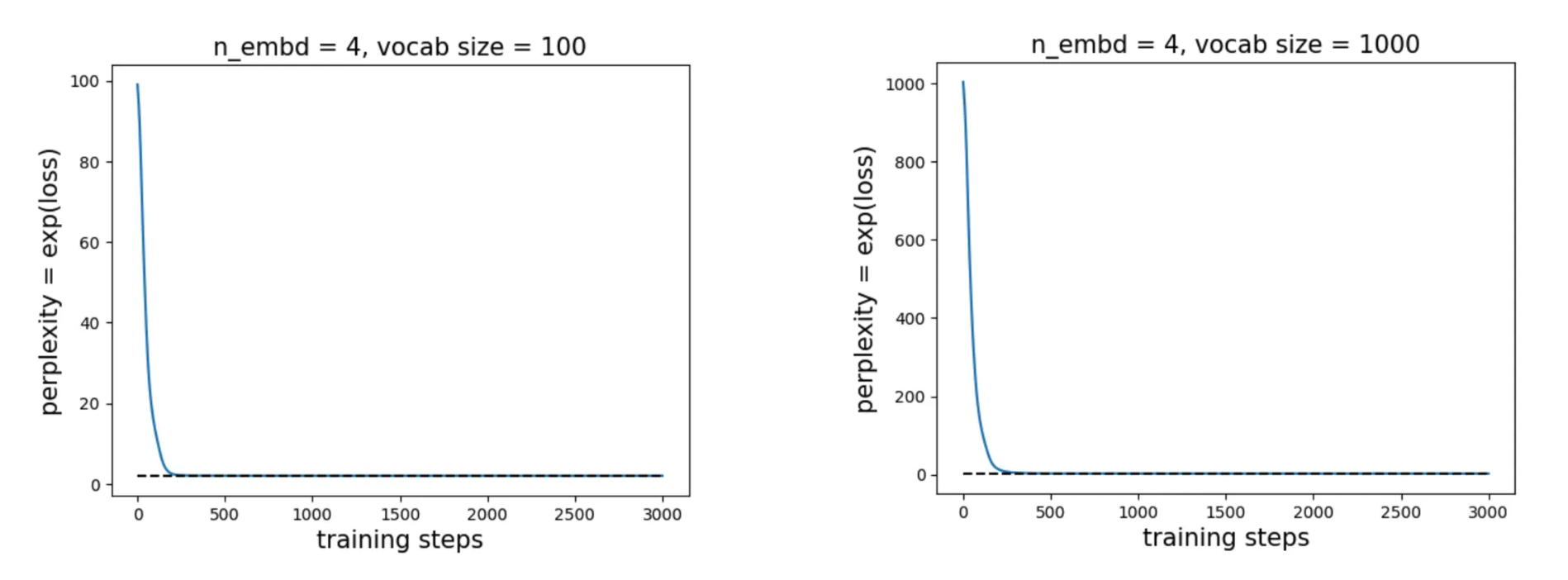
Moreover, the required embedding dimension appears to be independent of vocabulary size. For example, with vocab sizes of 100 or even 1000, the model still achieves the optimal perplexity of 2 with \(n_{\rm embd} = 4\).

However, once the embedding dimension reaches 4, the learned geometry becomes harder to interpret directly. Further study is needed. One possible hypothesis involves nearest-neighbor hopping: if we allow hopping to the nearest \(k\) neighbors, perhaps the required embedding dimension scales as \(2k\).

To probe this further, we now study an even simpler dataset with a deterministic drift.

Observation 2: existence of many equivalent embeddings

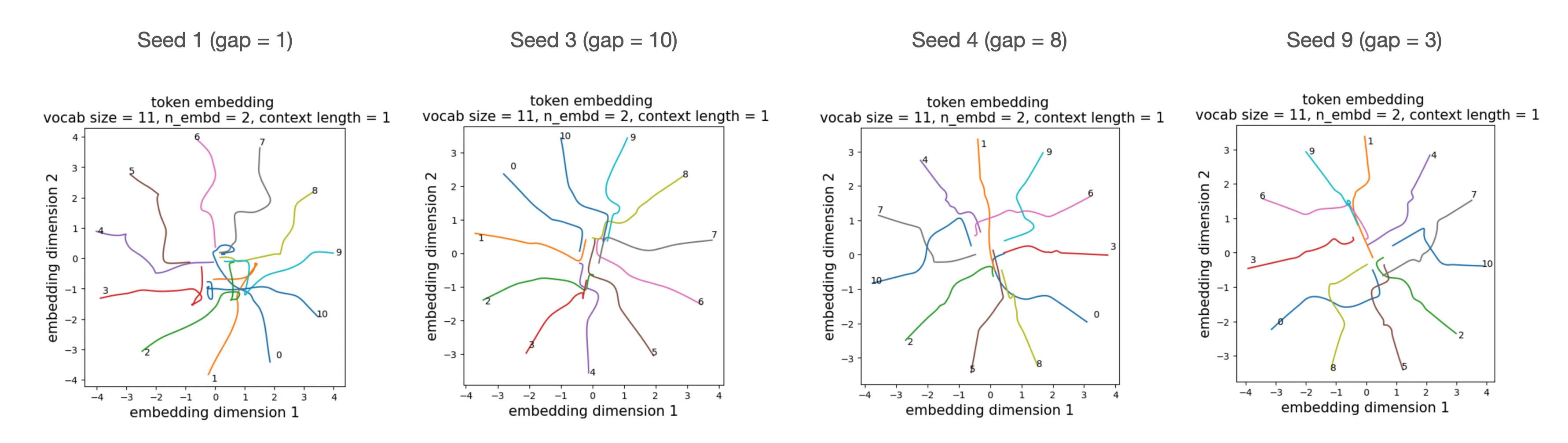
Dataset We restrict the walk to move only to the right. For example, \([5]\) can only transition to \([6]\) and never to \([4]\). In this case, the prediction task becomes deterministic. We find that \(n_{\rm embd} = 2\) is sufficient to achieve zero loss and perplexity 1.

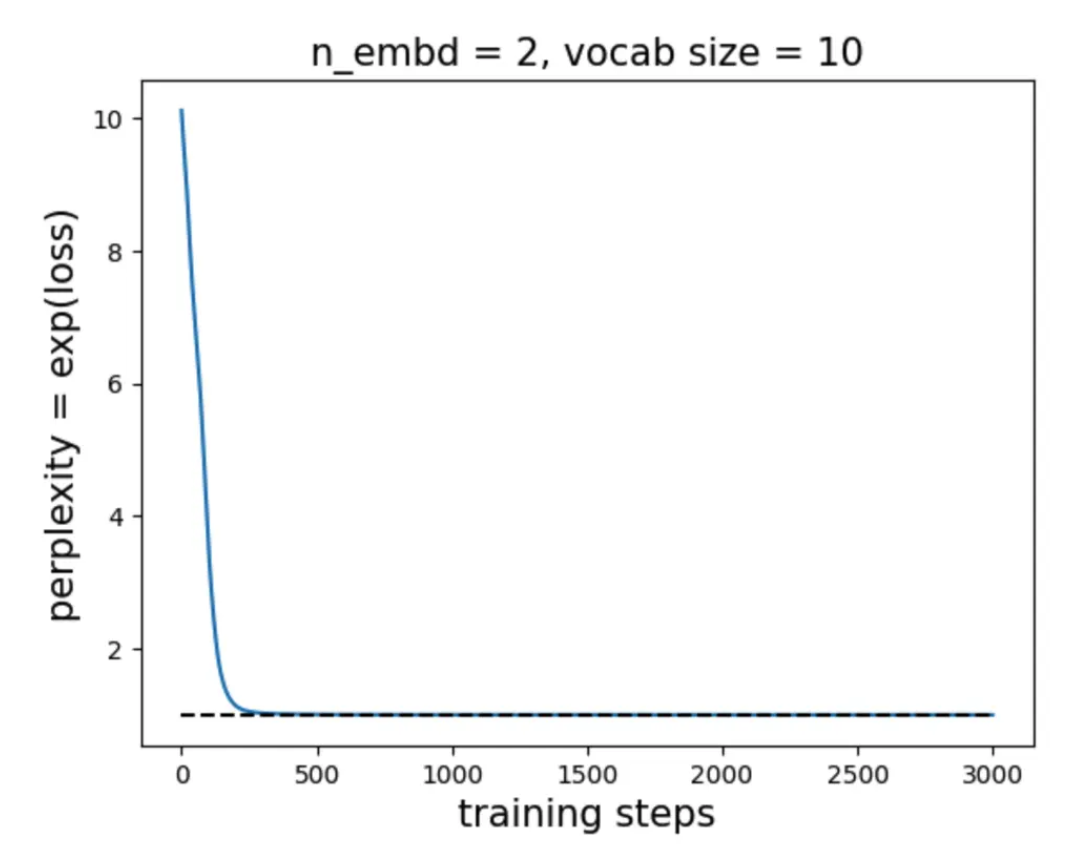
Interestingly, there are many equivalent embedding configurations that solve this task, and the model converges to one of them depending on initialization.

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026bigram-1,
  title={Bigram 1 -- Walk on a Circle},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/bigram-1/}
}