Representation anisotropy from nonlinear functions

Author: Ziming Liu (刘子鸣)

Motivation

Neural representations in deep neural networks are usually anisotrophic. This article aims to understand how nonlinear activation functions lead to representation anisotropy.

Toy model

We consider an LNL (linear-nonlinear) model, which is basically a two-layer MLP excluding the down projection layer: \(h_{\rm pre} = Wx, h_{\rm post} = \sigma(h_{\rm pre})\) where \(\sigma(\cdot)\) is the activation function. We set \(x\in\mathbb{R}^d\) to be isotropic – \(N\) samples are drawn from standard Gaussian distribution. \(W\in\mathbb{R}^{d\times D}\) is randomly initialized. We set \(d=100, D=400, N=10000\). We won’t train the model, and will only be interested in characterizing the anisotropy of \(h_{\rm post}\). We can stack \(h_{\rm post}\) of all \(N\) samples into a matrix \(H\in\mathbb{R}^{N\times D}\).

To measure anisotropy, we apply singular value decomposition (SVD) to \(H\) to obtain singular values. The singular value distribution characterizes anisotropy of representations. We normalize singular values so that they sum up to 1.

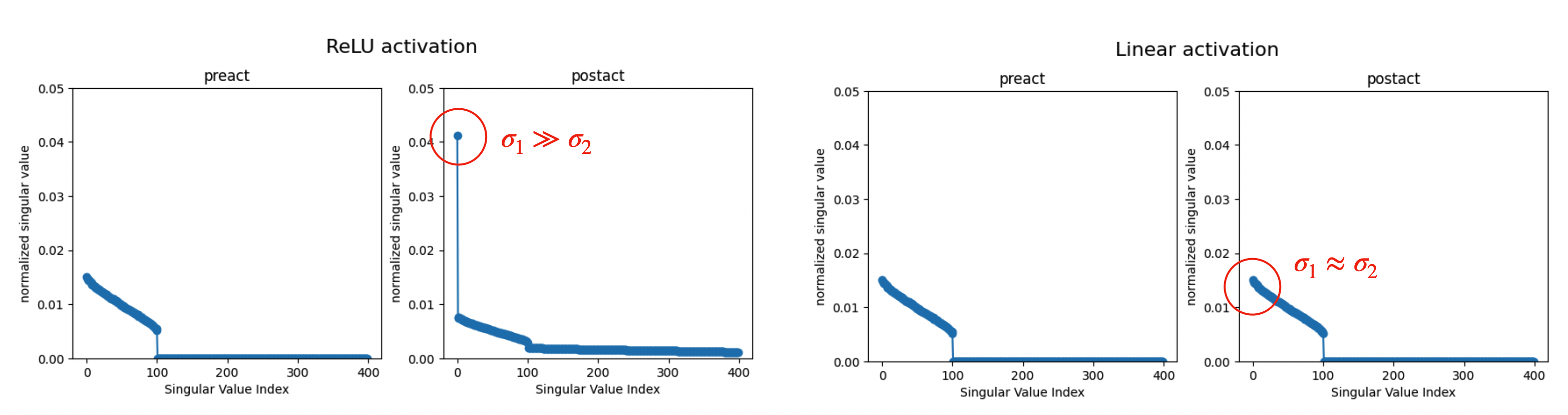
Observation 1: ReLU activation leads to massive \(\sigma_1\), while linear activation does not.

ReLU function make \(\sigma_1\) stand out, but linear function does not:

ReLU and linear:

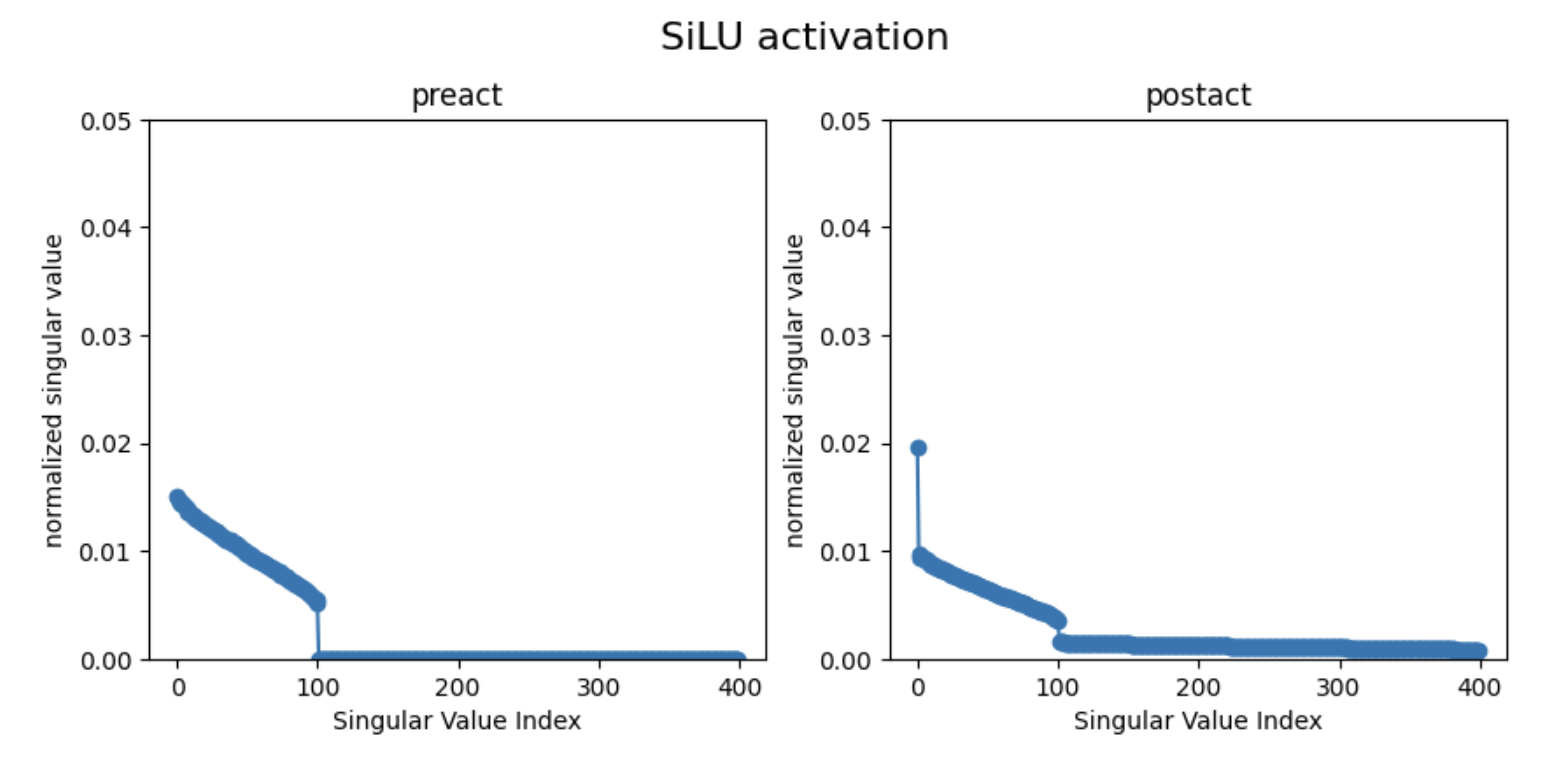
SiLU is qualitatively similar to ReLU:

This begs the question: why? Before answering why, we first do an interpolation experiment – leaky relu interpolates between ReLU (\(p=0\)) and linear (\(p=1\)). We will use the ratio \(\sigma_1/\sigma_2\) to measure how “standing out’’ \(\sigma_1\) is.

Observation 2: First order phase transition of Leaky ReLU

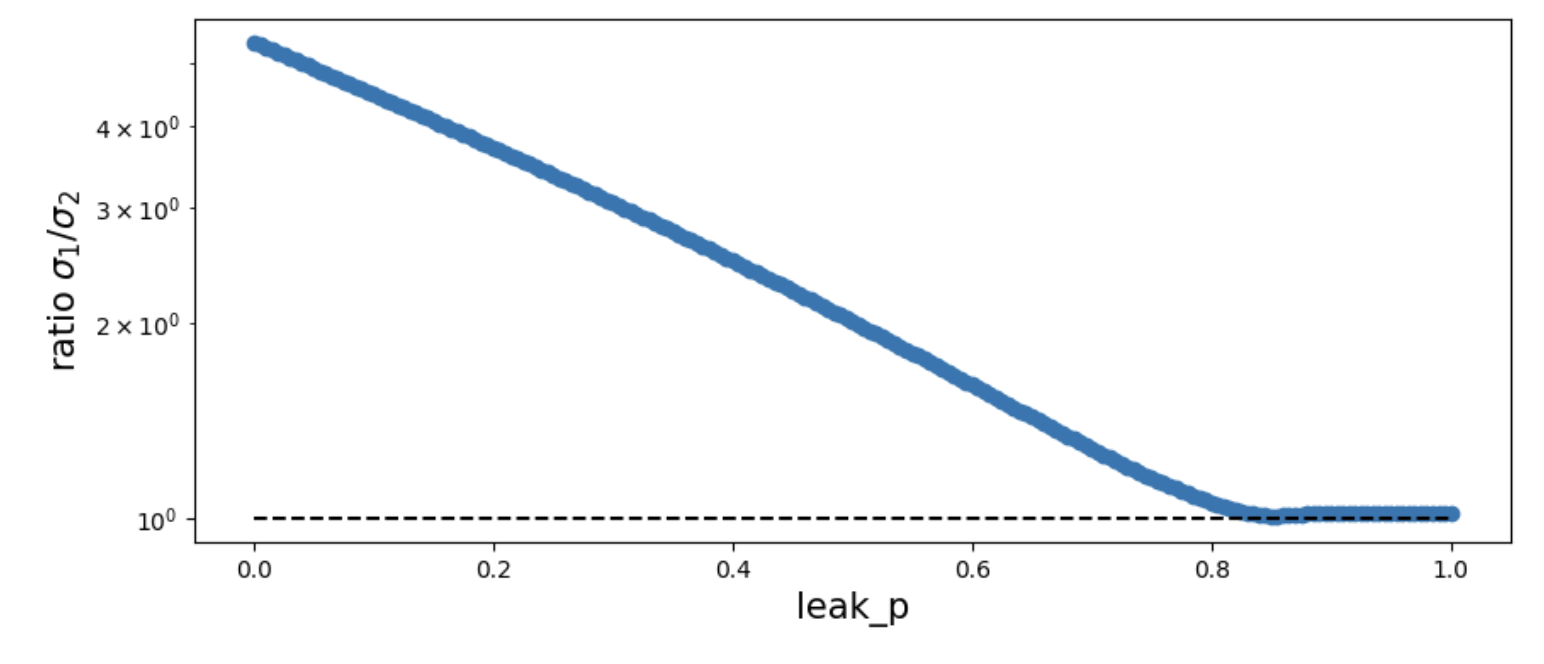
Although I expect that \(\sigma_1/\sigma_2\) would smoothly interpolate between two extremes, there is a first order phase transition around \(p_c\approx 0.8\). For \(p>p_c\), the ratio remains close to 1. For \(p<p_c\), the ratio grows exponentially (the y axis is log-scale) as \(p\) decreases. I don’t understand why.

Explanation: ReLU polarizes activations

The intuition: because ReLU maps negative values to zero, this creates a notion of polarity. Indeed, we find the first eigenvector to be \([1, 1, 1, \cdots, 1]\).

To better see this, we even drop the linear matrix and only keep the nonlinearity. For isotropic pre-activations, the spectrum for the post-activations look like this:

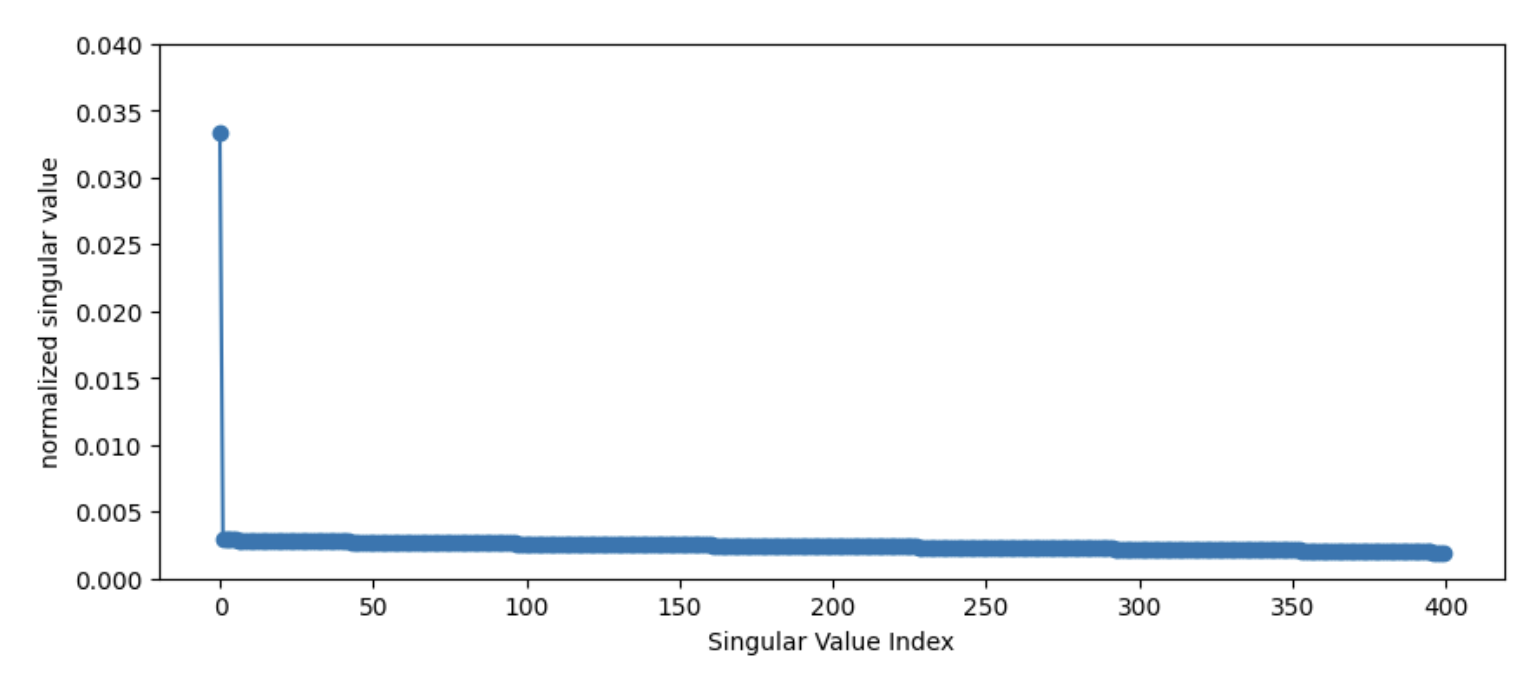
where \(\sigma_1\) stands out, while all rest singular values are small and almost the same.

In hindsight, this explantion is almost trivial, but the consequence (large \(\sigma_1\)) is something I don’t think I had appreciated enough.

Observation 3: Tanh doesn’t make \(\sigma_1\) stand out

Based on the above explantion, non-polarized activation functions (like Tanh) don’t make \(\sigma_1\) stand out, which is indeed the case:

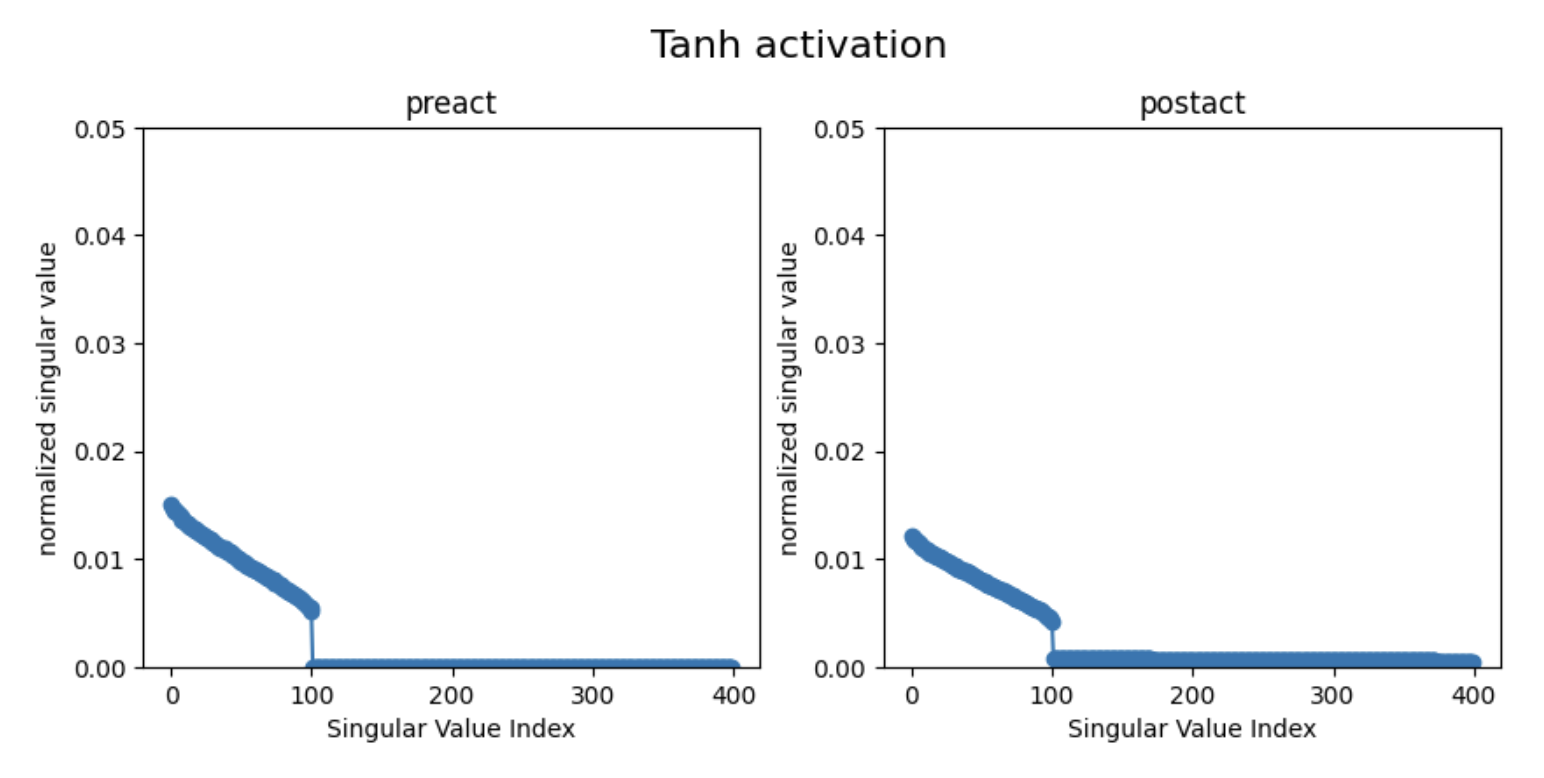
Question

• Is this a feature or a bug? Right now I tend to think this is a bug. Anisotropy could be the reason for training inefficiency.
• If this is a bug, how can we avoid this? Can we simply try to find better activation functions, or do we need extra processing?

Code

Google Colab notebook available here.

Citation

If you find this article useful, please cite it as:

BibTeX:

@article{liu2026activation-anisotropy,
  title={Representation anisotropy from nonlinear functions},
  author={Liu, Ziming},
  year={2026},
  month={January},
  url={https://KindXiaoming.github.io/blog/2026/activation-anisotropy/}
}