Philosophical thoughts on Kolmogorov-Arnold Networks

Recently, collaborators and I proposed a new type of neural networks called the Kolmogorov-Arnold Networks (KANs), which are somewhat similar to but mostly different from Multi-Layer Perceptrons (MLPs).

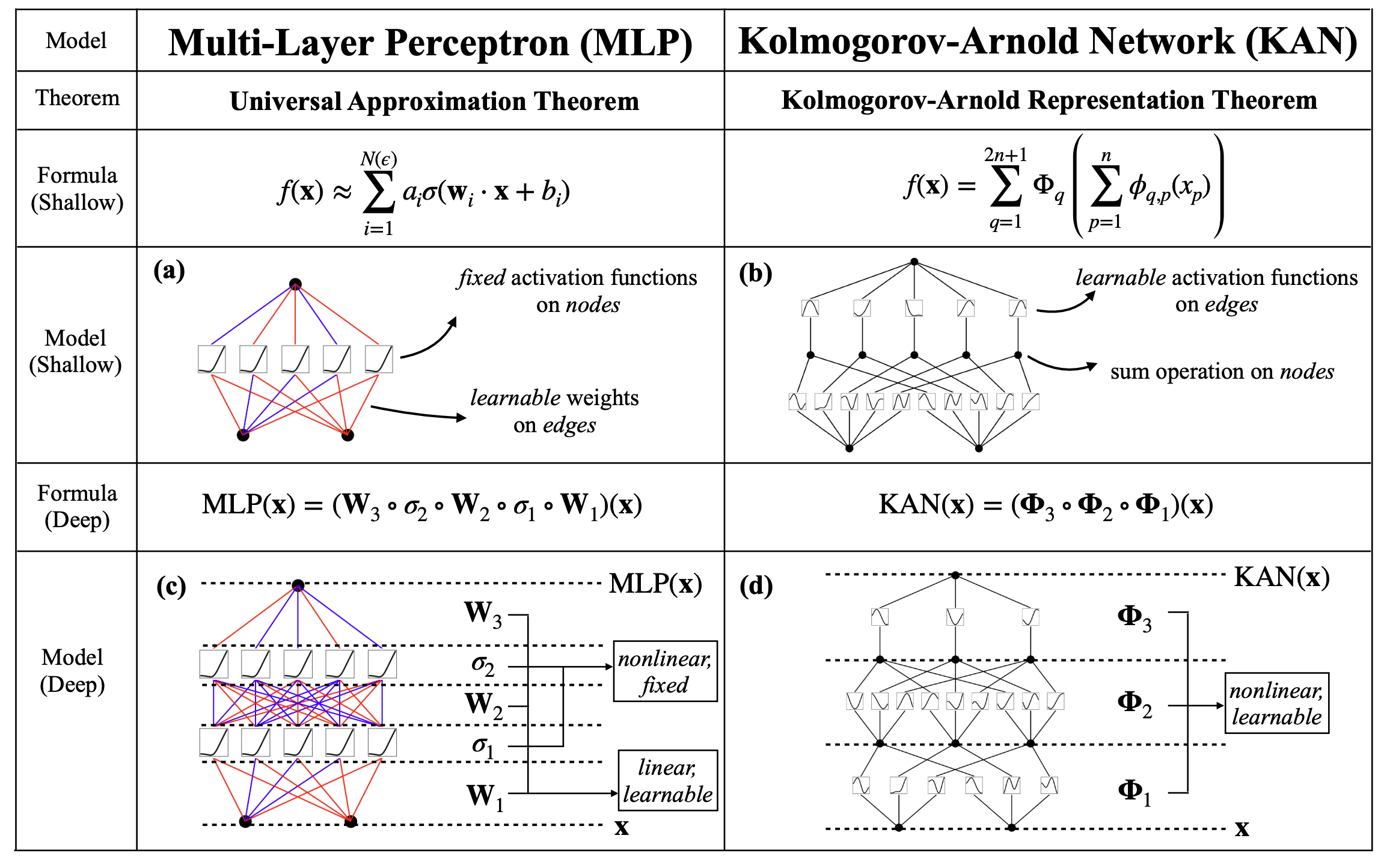
The technical differences between MLPs and KANs can be found in our paper and many discussions over the internet. This blogpost does not delve into technicalities, but want to lay out quick philosophical thoughts, open to discussion. I will attempt to answer the follwoing questions:

• Q1: Are KANs and MLPs the same?
• Q2: What’s the philosophical difference between KANs and MLPs?
• Q3: Which is more aligned with science, KANs or MLPs?

Q1: Are KANs and MLPs the same?

The argument that “KANs and MLPs are the same because they have the same expressive power” is similar to the argument “A human being and a cup are the same because they are both made up of atoms.” It is well accepted in physics that each (energy) level has a physical theory, so even if two systems share the same theory in the most microscopic level, they are not necessarily the same on higher levels because of emeregent phenomenon. Back to the MLPs vs KANs case, even though MLPs and KANs have the same expressive power (which is a foundational aspect), other aspects emerging from it might be quite different. These emerging properties include optimization, generalization, interpretability, etc.

Q2: What’s the philosophical difference between KANs and MLPs?

Reductionism vs. Holism While MLPs are more aligned with holism, KANs are more aligned with reductionism. The design principle of MLPs is “more is different”. In an MLP, each neuron is simple because it has fixed activation functions. However, what matters is the complicated connection patterns among neurons. The magical power of MLPs performing a task is an emergent behavior which is attributed to collective contribution from all neurons. By contrast, in a KAN, each activation function is complicated because it has learnable functions. By sparsification and pruning, we hope the computation graph to be simple. In summary, MLPs have simple ‘atoms’ but complicated ways to combine these atoms; KANs have complicated (diverse) ‘atoms’ but simple ways to combine these atoms. In this sense, MLPs’ expressive power comes from the complicated connection patterns (fully-connected structure), which give rise to emergent bahavior (holism). In contrast, KANs’ expressive power comes from the complexity of fundamental units (learnable activation functions), but the way to decompose whole network to units is simple (reductionsim).

Q3: Which is more aligned with science, KANs or MLPs?

We ask a crazy question: if our science is written by a neural network, is it more likely to be generated with KANs or with MLPs? I tend to say KANs are more aligned with our science. Note that the way we write science, is mostly based on reductionism. Throughout the history of science, reducntionism has been the standard way of thinking. It was not until very recently did scientists start to realize the importance of holism (“more is different”), however, the study of complex systems is extremely hard and many tools are still based on reductionism. Because our science is mostly reductionism, and KANs are more aligned with redunctionsim than MLPs, KANs are more promising tools to describe science. If you think the above discussion is too abstract, let us just consider a concrete task of compiling a symbolic formula into neural networks. Given the formula of Hooke’s law \(F=kx\), it is unclear how to compile this formula into MLPs with (say) ReLU activations, but it is quite straight-forward to compile it into KANs by leveraging flexiable activation functions. For example \(kx=((k+x)^2-k^2-x^2)/2\) can be represeted as a \([2,2,1]\) KAN; when both \(k, x\) are postive, we even just need a \([2,1,1]\) KAN by leveraging \(kx={\rm exp}({\rm log}k+{\rm log}x)\).

Closing Remarks

A model performs well on a task, when the inductive bias of the model meets the inductive bias of the task. So there is no free lunch – because KANs are good at science, there must be something KANs are not good at. MLPs are not good at science, people have shown their effectivenss on many non-scientific tasks including vision and languages. Trained as a physicist, I tend to think in redunctionsim. I constantly think about how a dataset can be generated from simple primitives (a process my advisor Max calls “braining”, i.e., training with my own brains), because it can inspire the design of better models. However, real world can be too complicated for my tiny brain to fully imagine and understand. Sometimes we just have to get our hands wet before burning out our brains. Combing back to the KAN vs MLP case, although I would love to understand their strengths and limitations with pure reasoning (philosophical thinking is one way), empirical experiments (guided by some reasoning) are probably more effective.